Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 270 271 272 273 274 275 276 >> Отображать по:
#111632
План обменов
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Дан массив. Ваша задача вывести план сортировки этого массива по неубыванию. Одно действие характеризуется двумя числами — индексами обмениваемых элементов. То есть, если выведено 1-3, это значит, что нужно поменять местами первый и третий элементы массива. Массив индексируется с единицы

Входные данные

В первой строке дано одно натуральное нечетное число n ( 1 ≤ n ≤ 10 4 ) — количество элементов массива. Во второй строке через пробел перечислены элементы массива — натуральные числа, не превышающие 10 9 .

Выходные данные

Выведите не более 10 5 строк, в каждой из которых выведите по два различных числа, разделенных дефисом — индексы обмениваемых ячеек. Если возможных ответов несколько — выведите любой.

Примеры
Входные данные
4
3 5 1 4
Выходные данные
3-1
3-2
4-3
#111634
Робот
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Студенты одного из вузов спроектировали робота для частичной автоматизации процесса сборки авиационного двигателя.

В процессе сборки двигателя могут встречаться операции 26 типов, которые обозначаются строчными буквами латинского алфавита. Процесс сборки состоит из N операций.

Предполагается использовать робота один раз для выполнения части подряд идущих операций из процесса сборки.

Память робота состоит из K ячеек, каждая из которых содержит одну операцию. Операции выполняются последовательно, начиная с первой, в том порядке, в котором они расположены в памяти. Выполнив последнюю из них, робот продолжает работу с первой. Робота можно остановить после любой операции. Использование робота экономически целесообразно, если он выполнит хотя бы K + 1 операцию.

Требуется написать программу, которая по заданному процессу сборки определит количество экономически целесообразных способов использования робота.

Входные данные

В первой строке входного файла записано число K > 0 "— количество операций, которые можно записать в память робота.

Вторая строка состоит из N > K строчных латинских букв, обозначающих операции "— процесс сборки двигателя. Операции одного и того же типа обозначаются одной и той же буквой.

Выходные данные

Выходной файл должен содержать единственное целое число "— количество экономически целесообразных способов использования робота.

Примечание

Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

  1. Тесты из условия. Подзадача оценивается в 0 баллов.

  2. N ≤ 100. Подзадача оценивается в 30 баллов.

  3. N ≤ 2000. Подзадача оценивается в 30 баллов.

  4. N ≤ 200 000. Подзадача оценивается в 40 баллов.

Примеры
Входные данные
2
zabacabab
Выходные данные
5
Входные данные
2
abc
Выходные данные
0
#111636
Древние династии
  

История Татаро-монгольского ханства богата на правителей. Каждый из N правителей принадлежал к одной из двух династий, причём власть часто переходила от одной династии к другой. Каждое восхождение правителя на престол отмечалось праздником, проводимым 26 марта. В летописях зафиксированы годы проведения этих праздников, причем известно, что правители первой династии устраивали для народа праздник кумыса, а второй — праздник мёда.

На конференции по истории Татаро-монгольского ханства каждый из S учёных предложил свою версию толкования летописи. А именно, i-й историк утверждал, что от каждого праздника кумыса до следующего праздника кумыса проходило не менее KLi лет, но не более KRi лет, в то время как от каждого праздника мёда до следующего праздника мёда проходило не менее MLi лет, но не более MRi лет.

Каждой предложенной версии может соответствовать несколько распределений правителей по династиям. Ученые договорились считать показателем сомнительности распределения число переходов власти к представителю той же самой династии.

Требуется написать программу, которая найдёт распределение, соответствующее хотя бы одной из версий и имеющее наименьший показатель сомнительности, а также версию, которой оно соответствует.

Входные данные

В первой строке входного файла записано число N (2 ≤ N ≤ 200 000) — количество праздников в летописи. Следующая строка содержит целые числа X1, X2, ..., XN (1 ≤ X1 ≤ X2 ≤ ... ≤ XN ≤ 109) — годы проведения праздников.

В третьей строке записано число учёных S (1 ≤ S ≤ 50). В каждой из последующих S строк записаны четыре натуральных числа KLi, KRi, MLi, MRi (1 ≤ KLi ≤ KRi ≤ 109), (1 ≤ MLi ≤ MRi ≤ 109).

Выходные данные

Первая строка выходного файла должна содержать числа P и Q, где P — номер учёного, версии которого соответствует распределение с наименьшим показателем сомнительности, а Q — показатель сомнительности этого распределения.

Вторая строка должна состоять из N цифр 1 и 2, записанных без пробелов, означающих приход к власти представителя первой или второй династии соответственно. Если существует несколько решений с наименьшим показателем сомнительности Q, выведите любое из них.

В случае, если ни в одной из версий учёных не существует способа распределения периодов правления между династиями так, чтобы не нарушались ограничения на промежутки времени между праздниками, выходной файл должен содержать единственное число 0.

Примечание

Данная задача содержит шесть подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

  1. Тесты из условия. Подзадача оценивается в 0 баллов.

  2. 2 ≤ N ≤ 15, 1 ≤ S ≤ 10. Подзадача оценивается в 20 баллов.

  3. 2 ≤ N ≤ 2000, 1 ≤ S ≤ 50, N × S ≤ 2000. Подзадача оценивается в 20 баллов.

  4. 2 ≤ N ≤ 10 000, 1 ≤ S ≤ 50, N × S ≤ 10 000. Подзадача оценивается в 20 баллов.

  5. 2 ≤ N ≤ 200 000, 1 ≤ S ≤ 50, N × S ≤ 200 000. Подзадача оценивается в 20 баллов.

  6. 2 ≤ N ≤ 200 000, 1 ≤ S ≤ 50. Подзадача оценивается в 20 баллов.

Примеры
Входные данные
3
1 2 3
1
1 1 1 1
Выходные данные
1 1
211
Входные данные
4
1 6 9 13
2
1 2 2 3
6 7 3 3
Выходные данные
0
Входные данные
5
3 6 8 9 10
2
2 3 1 1
1 4 1 10
Выходные данные
2 0
21212
#111639
От списков смежности к матрице смежности
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Простой неориентированный граф задан списками смежности, выведите его представление в виде матрицы смежности.

Входные данные

В первой строке входного файла задано одно целое число N ( 1 ≤ N ≤ 100 ) — число вершин. Далее в N строках содержатся списки смежности, в i -ой строке список смежности для i - 1 вершины. Каждая строка начинается с целого неотрицательного числа — длины списка. Далее в этой же строке через пробел перечислены все элементы списка. Гарантируется, что введенный граф корректен.

Выходные данные

В выходной файл выведите матрицу смежности графа.

Примеры
Входные данные
4
1 2
2 1 3
1 2
0
Выходные данные
0 1 0 0
1 0 1 0
0 1 0 0
0 0 0 0
#111640
От списка ребер к спискам смежности
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Простой неориентированный граф задан списком ребер, выведите его представление в виде списков смежности

Входные данные

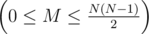В первой строке входного файла заданы два целых числа N ( 1 ≤ N ≤ 100 ) — число вершин и M — число ребер. Далее в M строках содержатся M пар чисел, каждая из которых описывает одно ребро графа. Гарантируется, что введённый список является корректным списком ребер некоторого неориентированного графа.

Выходные данные

В выходной файл выведите матрицу смежности графа в следующем формате. Для каждой вершины выведите сначала количество смежных вершин, а потом перечислите их в этой же строке через пробел. В i -ой строке должно быть описание i -ой вершины.

Примеры
Входные данные
3 2
1 2
2 3
Выходные данные
1 2
2 1 3
1 2
Страница: << 270 271 272 273 274 275 276 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест