Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 274 275 276 277 278 279 280 >> Отображать по:
#111710
Дороги
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes

Мэр города Гадюкино решил проверить состояние дорог после только что проведенного капитального ремонта. Для этого он хочет проехать по каждой дороге в обоих направлениях.

Помогите мэру составить кратчайший маршрут, проходящий по каждой дороге в каждом направлении хотя бы один раз.

Входные данные

В городе Гадюкино n перекрестков и m дорог, каждая из которых соединяет два различных перекрестка. Между двумя перекрестками может быть не более одной дороги.

Известно, что по дорогам от каждого перекрестка можно доехать до любого другого.

Входной файл содержит целые числа n и m (1 ≤ n ≤ 104, 1 ≤ m ≤ 105), и далее m пар целых чисел ai и bi — номера перекрестков, которые соединяет i-я дорога.

Выходные данные

Выведите число s — минимальную длину пути и далее s + 1 число — номера перекрестков в том порядке, в котором их нужно проезжать.

Примеры
Входные данные
3 3
1 2
2 3
1 3
Выходные данные
6
1 3 2 1 2 3 1
#111711
Dynamic LCA
  

Постановка задачи о {Наименьшем общем предке} такова: дано дерево T с выделенным корнем и две вершины u и v, lca(u, v) - вершина с максимальной глубиной, которая является предком и u, и v. Например, в картинке внизу lca(8, 7) - вершина 3.

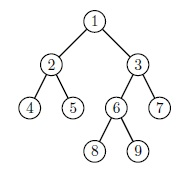
С помощью операции chroot(u) мы можем менять корень дерева, достаточно отметить u, как новый корень, и направить ребра вдоль пути от корня. Наименьшие общие предки вершин поменяются соответствующе. Например, если мы сделаем chroot(6) на картинке сверху, lca(8, 7) станет вершина 6. Получившееся дерево изображено снизу.

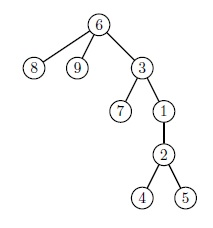
Вам дано дерево T. Изначально корень этого дерева - вершина 1. Напишите программу, которая поддерживает эти две операции: lca(u, v) и chroot(u).

Входные данные

Входной файл состоит из нескольких тестов.

Первая строка каждого теста содержит натуральное число n  — количество вершин в дереве (1 ≤ n ≤ 100 000). Следующие n - 1 строки содержат по 2 натуральных числа и описывают ребра дерева. Далее идет строка с единственным натуральным числом m — число операций —. Следующие m строк содержат операции. Строка "? u v" означает операцию lca(u, v), a строка "! u" - chroot(u). Последняя строка содержит число 0.

Сумма n для всех тестов не превосходит 100 000. Сумма m для всех тестов не превосходит 200 000.

Выходные данные

Для каждой операции "? u v" выведите значение lca(u, v). Числа разделяйте переводами строк.

Система оценки:

Система тестов состоит из двух групп:

Первая группа состоит из тестов, для которых выполняется ограничение \(n \le 100\), \(m \le 10000\). За прохождение всех тестов группы ставится 55 баллов.

Вторая группа стоит из тестов, в которых нет дополнительных ограничений. За прохождение тестов этой группы и всех предыдущих тестов ставится дополнительно 45 баллов.

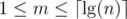Примеры
Входные данные
9
1 2
1 3
2 4
2 5
3 6
3 7
6 8
6 9
10
? 4 5
? 5 6
? 8 7
! 6
? 8 7
? 4 5
? 4 7
? 5 9
! 2
? 4 3
0
Выходные данные
2
1
3
6
2
3
6
2
#111712
Распил брусьев
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вам нужно распилить деревянный брус на несколько кусков. Компания берет плату за пилку в зависимости от размера бруса, который нужно распилить. За разрезание бруса длиной l берется l у.е.

Легко понять, что различные заказы приводят к различным ценам. Найдите минимальную стоимость распила для любого бруса заданного размера.

Входные данные

В первой строке число L(1 ≤ L ≤ 1000) — начальная длина бруса, следующая строка содержит число распилов n(1 ≤ n ≤ 160), которые нужно сделать. Следующая строка содержит n положительных чисел (0 ≤ ci ≤ L) — места, в которых нужно сделать распилы.

Выходные данные

Выведите минимальную стоимость распила.

Примеры
Входные данные
10
3
2 4 7
Выходные данные
20
Входные данные
100
3
25 50 75
Выходные данные
200
#111715
Машина арифметика
  
ограничение по времени на тест
3.5 second;
ограничение по памяти на тест
64 megabytes

Миша записывает 2 числа: n и m, а Маша должна разделить число n на m частей, не меняя порядок цифр, при этом Миша ещё требует, чтобы произведение полученных m чисел было максимально. Помогите Маше.

Входные данные

Входные данные содержат несколько тестовых случаев (не более 100000). Каждый тестовый случай расположен в отдельной строке и содержит 2 числа, разделённые пробелом: сначала n (1 ≤ n ≤ 1015), а потом m ().

Выходные данные

Для каждого тестового примера в отдельной строке выведите искомое максимальное произведение.

Примеры
Входные данные
12345 2
12345 3
Выходные данные
6170
2460
#111716
Вопль
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

Вожди известного племени Мумба-Юмба решили придумать новый боевой вопль для своих воинов. При этом они решили, что вопль должен состоять ровно из N букв (всего в алфавите племени M букв). Также, после долгих исследований было выяснено, что если в вопле встречается слово si (слово – это последовательность букв алфавита, не длиннее трех символов), то этот вопль вселяет во врага fi единиц страха. Если в вопль входит несколько слов, то их “страшность” суммируется. Например, если вопль содержит слова si и sj, то вопль вселяет fi+fj единиц страха.

Требуется по заданным N, M, алфавиту и списку слов si составить максимально страшный вопль.

Входные данные

В первой строке записано три числа — N, M и К (1 ≤ N ≤ 100, 1 ≤ M ≤ 24, 0 ≤ K ≤ 100), где K — количество страшных слов. В следующей строке записан алфавит — строка из M строчных латинских букв. Далее в K строках записана информация о словах — само слово и через пробел одно число, обозначающее страшность этого слова (1 ≤ fi ≤ 10000).

Выходные данные

В выходной файл необходимо вывести страшность полученного вопля и на следующей строке — сам вопль.

Примеры
Входные данные
3 5 4
abcde
abc 10
ab 5
be 7
e 4
Выходные данные
16
abe
Страница: << 274 275 276 277 278 279 280 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест