Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 275 276 277 278 279 280 281 >> Отображать по:
#111717
Башня
  
ограничение по времени на тест
0.25 second;
ограничение по памяти на тест
64 megabytes

Воодушевленный легендой о Вавилонской Башне, Петя решил построить ее аналог у себя в комнате, для этого он взял N детских строительных кирпичиков, выбрал для себя размер основания D и высоту башни H. Кроме того, он решил для себя, что размер каждого следующего уровня будет отличаться от предыдущего на один. Башня, показанная на рисунке, удовлетворяет Петиным запросам, имеет основание 2, высоту 8, и составлена из 22 кирпичиков.

Ваша задача состоит в том, чтобы написать программу, которая определяет, можно ли построить башню при выбранных Петей параметрах, и если да, то выдает сколько кирпичей должно быть на каждом уровне.

Входные данные

Во входном файле находятся числа N, D, и H (в таком порядке), разделенные пробелами (1 ≤ N ≤ 1 000, 1 ≤ D, H ≤ 30)

Выходные данные

Если башня, удовлетворяющая Петиным запросам существует, выведите в выходной файл H чисел — проект любой такой башни — количество кирпичиков на каждом уровне, начиная с самого нижнего. В противном случае выведите 0.

Примеры
Входные данные
22 2 8
Выходные данные
2
3
4
3
4
3
2
1
Входные данные
6 3 2
Выходные данные
0
#111718
Пересечение
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Компания, производящая оборудование для сотовой связи, обратилась к вам с просьбой написать программу, оценивающую качество организации сети. Одним из важных параметров является то, пересекаются ли зоны покрытия передатчиков, работающих на одинаковых частотах. Для простоты будем считать, что область покрытия каждого передатчика представляет собой многоугольник на плоскости (не обязательно выпуклый). Две области покрытия будем считать пересекающимися, если у них есть хотя бы одна общая точка (возможно, лежащая на границе одной или даже обеих областей). Ваша программа должна принимать на вход набор пар многоугольников, описывающих зоны покрытия передатчиков, и выводить про каждую пару информацию о том, пересекаются ли эти зоны.

Входные данные

На первой строке входного файла находится число K — количество тестов во входном файле. Далее идёт описание K тестов. Каждый тест задаётся описанием двух многоугольников, которые надо проверить на пересечение. Каждый многоугольник задаётся в следующем формате: сначала указывается одно число Ni — число вершин этого многоугольника, — после чего идут Ni строк, каждая из которых содержит два разделённых пробелом числа xij и yij — координаты j-й вершины этого многоугольника. Вершины перечислены в порядке обхода многоугольника.

Число пар многоугольников в одном тесте 1 ≤ K ≤ 10, число вершин каждого многоугольника 3  ≤  Ni  ≤  100, координаты вершин — целые числа,  - 10 000 ≤ xij, yij ≤ 10 000.

Выходные данные

Для каждой пары многоугольников выведите в выходной файл на отдельной строке одно слово: "YES", если многоугольники пересекаются, и "NO", если нет.

Примеры
Входные данные
2
3
0 0
-1 0
0 -1
3
1 1
2 1
1 2
4
0 0
2 0
2 2
0 2
4
1 1
3 1
3 3
1 3
Выходные данные
NO
YES
#111720
Машина арифметика
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes

Миша записывает 2 числа: n и m, а Маша должна разделить число n на m частей, не меняя порядок цифр, при этом Миша ещё требует, чтобы произведение полученных m чисел было максимально. Помогите Маше.

Входные данные

Входные данные содержат несколько тестовых случаев (не более 100000). Каждый тестовый случай расположен в отдельной строке и содержит 2 числа, разделённые пробелом: сначала n (1 ≤ n ≤ 1015), а потом m ().

Выходные данные

Для каждого тестового примера в отдельной строке выведите искомое максимальное произведение.

Примеры
Входные данные
12345 2
12345 3
Выходные данные
6170
2460
#111722
Задача о рюкзаке
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Одной из классических NP-полных задач является так называемая «Задача о рюкзаке». Формулируется она следующим образом. Дано n предметов, каждый из которых характеризуется весом wi и полезностью pi. Необходимо выбрать некоторый набор этих предметов так, чтобы суммарный вес этого набора не превышал W, а суммарная полезность была максимальна. Ваша задача состоит в том, чтобы написать программу, решающую задачу о рюкзаке.

Входные данные

Первая строка входного файла содержит натуральные числа n(1 ≤ n ≤ 20) и W(1 ≤ W ≤ 109). Каждая из последующих n строк содержит описание одного предмета. Каждое описание состоит из двух чисел: wi — веса предмета и pi — его полезности (1 ≤ wi, pi ≤ 109).

Выходные данные

В первой строке выходного файла выведите количество выбранных предметов и их суммарную полезность. Во второй строке выведите через пробел их номера в возрастающем порядке (предметы нумеруются с единицы в порядке, в котором они перечислены во входном файле). Если искомых наборов несколько, выберите тот, в котором наименьшее число предметов. Если же после этого ответ по-прежнему неоднозначен, выберите тот набор, в котором первый предмет имеет наименьший возможный номер, из всех таких выберите тот, в котором второй предмет имеет наименьший возможный номер, и т. д.

Примеры
Входные данные
2 10
10 100
9 80
Выходные данные
1 100
1
Входные данные
5 100
80 1000
50 550
50 550
50 550
50 550
Выходные данные
2 1100
2 3
Входные данные
6 100
80 1000
50 550
50 550
50 550
50 550
100 1100
Выходные данные
1 1100
6
#111723
Network Instability
  

Вася устроился сисадмином в крупную и известную компанию Проблемсофт. В сети компании n компьютеров, некоторые пары которых соединены кабелем напрямую. Всего таких соединений m, причем Вася весьма неплохой администратор, так что никакой кабель не соединяет компьютер с самим собой и каждая пара компьютеров соединена не более чем одним кабелем.

На каждом компьютере в фирме Проблемсофт установлена специальная программа разработанная и поддерживаемая инженерами Проблемсофта, под названием ЗлойЖук. Инженеры этой компании отличаются крайним трудолюбием и высокой производительностью, в связи с чем новые версии программы ЗлойЖук выходят почти ежедневно. Однако, не все сотрудники компании разделяют трудолюбие инженеров, поэтому обновляют программу ЗлойЖук неохотно, и всякий раз до какой-то случайной версии (вполне могут "обновить" до такой же или даже более старой).

После нескольких ужасных месяцев, в течение которых исправлять различные ошибки приходилось днями и ночами, без обедов и выходных, Вася понял в чем причина подавляющего большинства всех сбоев! Причина в том, что компьютеры пересылающие данные по соединяющему их кабелю могут иметь различные версии программы ЗлойЖук. Прямое соединение кабелем двух компьютеров с различными версиями программы ЗлойЖук Вася называет нестабильным.

На последнем корпоративе компании Проблемсофт Вася вместо развлечений ходил с листочком и узнавал у каждого сотрудника когда он планирует обновить программу ЗлойЖук и до какой версии. Нельзя сказать, чтобы коллеги охотно отвечали на эти вопросы, вместо того что купаться в джакузи и пить Кока-Колу, но все-таки Вася смог составить график планируемых изменений версий программы ЗлойЖук на всех компьютерах сети Проблемсофта. Теперь его интересует количество нестабильных соединений в сети после выполнения каждого изменения.

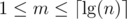Входные данные

Первая строка входного файла содержит два целых числа n и m (1 ≤ n, m ≤ 105).

Вторая строка содержит n целых чисел v1, v2, ..., vn: версии программы ЗлойЖук изначально установленные на компьютерах Проблемсофта (1 ≤ vi ≤ 105).

Следующие m строк содержат числа ai и bi: описание соединений (1 ≤ ai, bi ≤ n, ai ≠ bi). Гарантируется что сеть хорошая, то есть никакая пара компьютеров не соединена более чем одним кабелем и никакой компьютер не соединен кабелем с самим собой.

Следующая строка содержит целое число q: количество запланированных изменений версий программы ЗлойЖук (1 ≤ q ≤ 105).

Далее следуют q строк; i-ая содержит числа ci и v'i: номер компьютера на котором происходит изменение, и номер новой версии программы ЗлойЖук. Изменения даны в хронологическом порядке, никакия два изменения не происходят одновременно.

Выходные данные

Выведите q строк; i-ая строка должна содержать одно целое число: количество нестабильных соединений сразу после выполнения i-го обновления.

Примеры
Входные данные
4 5
1 2 3 4
1 2
2 3
3 4
4 1
1 3
5
1 5
3 2
4 4
1 4
2 3
Выходные данные
5
4
4
3
4
Страница: << 275 276 277 278 279 280 281 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест