Вы с друзьями играете в следующую игру. Друзья пишут на доске подряд N натуральных чисел. Ваша задача — найти как можно больше подряд идущих чисел, которые бы делились на одно и то же число, большее 1. Так как вручную искать ответ сложно, вы решили написать программу, которая сделает работу за вас.

Охотник Боб часто гуляет со своей собакой Ральфом. Боб гуляет с постоянной скоростью и его путь – ломаная (возможно, самопересекающаяся), каждая вершина которой задается двумя целыми числами (X_i, Y_i) – декартовыми координатами.

Ральф бегает сам по себе, но обязательно должен встречаться с хозяином в указанных N точках. Собака начинает свой путь одновременно с хозяином в точке (X₁, Y₁) и завешает его вместе с хозяином в точке (X_N, Y_N).

Ральф может бегать с любой скоростью, не превышающей в два раза скорость Боба. Пока Боб идет по прямой из точки в точку, собака ищет деревья, кусты, холмики и прочие интересные места, которые заданы парами целых чисел (X^'_j, Y^'_j). Всего таких мест M. Тем не менее, покидая своего хозяина в точке (X_i, Y_i) (где 1 ≤ i ≤ N), Ральф посещает не более одного интересного места перед тем, как опять встретить хозяина в точке (X_i + 1, Y_i + 1).

Ваша задача – найти маршрут, удовлетворяющий указанным выше условиям, с максимальным количеством посещаемых интересных мест. Он представляется ломаной, по которой бегает Ральф. Ее вершинами должны быть все точки (X_i, Y_i) и посещенные интересные места (X^'_j, Y^'_j). Последние должны быть посещены (то есть встречаться в описании пути) не более одного раза.

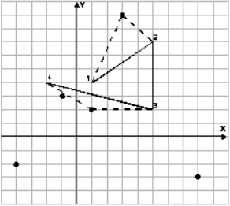
Пример пути Боба (сплошная линия), набора интересных мест (точки) и одного из лучших путей Ральфа представлены на рисунке:

У Егора очень старый телефон. Слава отправил Егору кодовую фразу от Серёжиного банковского счёта, чтоб его ограбить, но телефон Егора настолько стар, что не умеет принимать длинные сообщения. Он разбивает их на несколько маленьких случайной длины, и приходят они ему в случайном порядке.

Когда Егор получил все эти сообщения, он по-настоящему расстроился. Он проклинал телефон, кидал его об стену. К несчастью, телефон оказался обидчивым и перемешал ещё и все буквы в каждом сообщении, хоть и склеил при этом все сообщения в одно. Егор знал, что Серёжа любит такие строки, что в них все буквы идут по убыванию (в обратном алфавитном порядке). Помогите Егору и Славе и найдите кодовую фразу от Серёжиного банковского счёта по единственному оставшемуся сообщению в телефоне.

Дано целое положительное число в десятичной записи. Рассмотрим числа, полученные из него циклическим сдвигом на 0,  1,  ...,  N - 1 цифр, и каждое из этих N чисел умножим на его первую цифру цифру. Требуется вывести сумму полученных произведений.

Недавно королева страны AlgoLand придумала новый способ отмывания денег для своего королевского двора. Она решила, что всякий житель, желающий совершить путешествие из одного города страны в другой, должен расплатиться за это желание своими деньгами.

В стране AlgoLand есть N городов, пронумерованных от 1 до N. Некоторые города соединены дорогами, движение по которым разрешено в двух направлениях. Начиная движение по какой-нибудь дороге, путешественник обязательно должен доехать до ее конца.

Предположим теперь, что житель страны хочет совершить путешествие из города A в город B. Новый указ королевы гласит, что при проезде по любой дороге страны во время этого путешествия, полицейские могут взять с этого жителя таможенную пошлину в пользу королевского двора (а могут и не взять). Если при этом у жителя недостаточно денег для уплаты пошлины, то он автоматически попадает в тюрьму. Указ также устанавливает величину пошлины для каждой дороги страны. Так как королева заботится о жителях своей страны, то она запретила полицейским брать с жителя пошлину более чем два раза во время одного путешествия.

Отметим, что если существует несколько способов попасть из города A в город B, то житель может выбрать для путешествия любой из них по собственному желанию.

Напишите программу, которая определяет, какую минимальную сумму денег должен взять с собой житель, чтобы гарантированно не попасть в тюрьму во время путешествия.