Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 294 295 296 297 298 299 300 >> Отображать по:
#112128
Аппликатура
  
ограничение по времени на тест
0.25 second;
ограничение по памяти на тест
256 megabytes

Одна из проблем при игре на фортепьяно — выбор хорошей «аппликатуры», то есть определение для каждого звука мелодии (клавиши инструмента) пальца руки, которым эту ноту лучше всего сыграть в данном месте мелодии.

Пронумеруем пальцы пианиста слева направо натуральными числами от 1 до P, клавиши инструмента также пронумеруем слева направо натуральными числами от 1 до K. Тогда запись звуков мелодии можно представить в виде последовательности N номеров клавиш, которые следует нажимать для ее исполнения, где N — длина мелодии.

Пусть для каждой пары пальцев с номерами i и j заданы целые числа aij и bij, такие, что если палец i нажимает клавишу X, то следующей клавишей пальцем j может быть нажата лишь клавиша из диапазона [X + aij, X + bij]. Этот набор чисел aij, bij, 1 ≤ i ≤ P, 1 ≤ j ≤ P, зависит от особенностей пианиста и его исполнительской техники. Заметим, что не каждая мелодия может быть сыграна конкретным пианистом при указанных выше ограничениях.

Назовем перекладыванием пальцев ситуацию, когда для двух последовательно исполняемых нот мелодии клавиша с большим номером нажимается пальцем с меньшим номером. Требуется написать программу, которая для заданной мелодии определяет аппликатуру с наименьшим количеством перекладываний пальцев.

Входные данные

В первой строке входного файла содержится число P — количество пальцев у пианиста (1 ≤ P ≤ 20). Во второй строке записано число K  —  количество клавиш у инструмента (1 ≤ K ≤ 10000). В третьей строке указаны целые числа a11b11a12b12...a1Pb1Pa21b21a22b22...a2Pb2P...aP1bP1aP2bP2...aPPbPP, разделенные пробелами ( - K ≤ aij ≤ bij ≤ K). В четвертой строке находится число N — длина мелодии (1 ≤ N ≤ 1000). Пятая строка содержит N чисел X1X2...XN — последовательность разделенных пробелами номеров клавиш для исполнения мелодии.

Выходные данные

В первой строке выходного файла должно содержаться либо число L — количество перекладываний пальцев в оптимальной аппликатуре, либо число  - 1 при невозможности сыграть мелодию. Вторая строка при наличии решения должна содержать N чисел Y1...YN — последовательность разделенных пробелами номеров пальцев при исполнении мелодии.

Примеры
Входные данные
3
10
0 0 -2 -2 -5 1 2 3 8 10 0 1 2 10 -2 -2 -1 -1
9
4 5 7 7 7 6 8 7 5
Выходные данные
3
1 3 1 1 3 3 1 3 2
#112335
Автомат с игрушками
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
256 megabytes
В развлекательном центре \(Е\)-города был установлен игровой автомат нового поколения. В автомат можно бросить монету и следить за её продвижением сверху вниз по разветвляющемуся лабиринту из трубок. В лабиринте есть n узлов, которые пронумерованы числами от 1 до \(n\). При бросании монета попадает в первый узел. Каждый узел лабиринта, кроме первого, имеет одну входящую сверху трубку, по которой монета может в него попасть. Из каждого узла выходит не более двух трубок, идущих вниз, одна из которых ведет налево, а другая — направо. Каждая трубка имеет некоторую ширину. Монета проваливается в более широкую трубку, а в случае равенства ширины трубок — в левую.

После прохождения монеты по трубке ширина этой трубки уменьшается на 1. Монета не может пройти по трубке ширины 0. Если монета достигла узла, из которого она не может дальше двигаться вниз, автомат останавливается и ждёт, когда в него бросят следующую монету

Изначально в каждом узле лабиринта находится по игрушке. Когда монета попадает в узел первый раз, игрушка, находящаяся в этом узле, достаётся игроку, бросившему эту монету.

Панкрату понравилась игрушка, которая находится в узле с номером \(v\).

Требуется написать программу, которая определяет, сколько монет должен бросить в автомат Панкрат, чтобы получить игрушку из узла \(v\).

Формат входного файла

В первой строке входного файла задано число \(n\) — количество узлов в лабиринте. В последующих n строках заданы описания всех узлов, в \(k\)-й из этих строк описан узел с номером \(k\).

Описание k-го узла состоит из четырех целых чисел: \(a_k\), \(u_k\), \(b_k\), \(w_k\). Если из \(k\)-го узла выходит левая трубка, то \(a_k\) — номер узла, в который она ведет (\(k\) < \(a_k\) <= \(n\)), а \(u_k\) — её ширина. Если левой трубки нет, то \(a_k\) = \(u_k\) = 0. Если из \(k\)-го узла выходит правая трубка, то \(b_k\) — номер узла, в который она ведет (\(k\) < \(b_k\) <= \(n\)), а \(w_k\) — её ширина. Если правой трубки нет, то \(b_k\) = \(w_k\) = 0.

В последней строке задано целое число \(v\) (1 <= \(v\) <= \(n\)) — номер узла, в котором находится игрушка, понравившаяся Панкрату.

Гарантируется, что во все узлы, кроме первого, входит ровно одна трубка

Формат выходного файла

Выходной файл должен содержать одно число — количество монет, которое необходимо бросить в автомат Панкрату, чтобы получить игрушку, которая находится в узле \(v\). Если получить выбранную игрушку невозможно, выведите число −1.

Система оценки

Данная задача содержит две подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 1

1 <= \(n\) <= 100

1 <= \(u_k\); \(w_k\) <= 300

Подзадача оценивается в 50 баллов.

Подзадача 2

1 <= \(n\) <= \(10^5\)

1 <= \(u_k\); \(w_k\) <= \(10^9\)

Подзадача оценивается в 50 баллов.

Пояснения к примеру

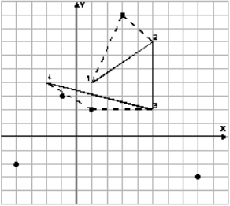
В первом примере первая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 1, 3 и 4:

Вторая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 2 и 6:

Третья монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 5 и 7:

Примеры
Входные данные
7
2 1 3 2
0 0 6 3
4 1 5 1
0 0 0 0
7 2 0 0
0 0 0 0
0 0 0 0
5
Выходные данные
3
Входные данные
4
0 0 2 1
4 1 3 1
0 0 0 0
0 0 0 0
3
Выходные данные
-1
#112516
The dog task
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

Охотник Боб часто гуляет со своей собакой Ральфом. Боб гуляет с постоянной скоростью и его путь – ломаная (возможно, самопересекающаяся), каждая вершина которой задается двумя целыми числами ( X i , Y i ) – декартовыми координатами.

Ральф бегает сам по себе, но обязательно должен встречаться с хозяином в указанных N точках. Собака начинает свой путь одновременно с хозяином в точке ( X 1 , Y 1 ) и завешает его вместе с хозяином в точке ( X N , Y N ) .

Ральф может бегать с любой скоростью, не превышающей в два раза скорость Боба. Пока Боб идет по прямой из точки в точку, собака ищет деревья, кусты, холмики и прочие интересные места, которые заданы парами целых чисел ( X ' j , Y ' j ) . Всего таких мест M. Тем не менее, покидая своего хозяина в точке ( X i , Y i ) (где 1 ≤ i ≤ N ), Ральф посещает не более одного интересного места перед тем, как опять встретить хозяина в точке ( X i + 1 , Y i + 1 ) .

Ваша задача – найти маршрут, удовлетворяющий указанным выше условиям, с максимальным количеством посещаемых интересных мест. Он представляется ломаной, по которой бегает Ральф. Ее вершинами должны быть все точки ( X i , Y i ) и посещенные интересные места ( X ' j , Y ' j ) . Последние должны быть посещены (то есть встречаться в описании пути) не более одного раза.

Пример пути Боба (сплошная линия), набора интересных мест (точки) и одного из лучших путей Ральфа представлены на рисунке:

Входные данные

На первой строке через пробел записаны два числа N и M (2 ≤ N ≤ 100, 0 ≤ M ≤ 100) . Вторая строка содержит N пар целых чисел X 1 , Y 1 , ..., X N , Y N , разделенных пробелом, описывающих путь Боба. В третьей строке записано M пар целых чисел, ( X ' 1 , Y ' 1 ) , ... ( X ' M , Y ' M ) , разделенных пробелом, описывающих интересные места.

Все точки в условии различны и координаты по модулю не превосходят 1000 .

Выходные данные

В выходном файле должно быть единственное число K – количество вершин в оптимальном маршруте Ральфа.

Примеры
Входные данные
4 5
1 4 5 7 5 2 -2 4
-4 -2 3 9 1 2 -1 3 8 -3
Выходные данные
6
#112519
Артемида
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Зевс подарил Артемиде, богине охоты, прямоугольный участок земли, чтобы вырастить лес. Левая сторона этого участка  — это отрезок неотрицательного луча оси ординат, нижняя сторона — отрезок неотрицательного луча оси абсцисс, а (0, 0) — левый нижний угол участка. Зевс сказал Артемиде выращивать деревья только в точках с целыми координатами.

Артемида любит, когда лес выглядит естественно, и поэтому в её лесу любая прямая, проходящая через два дерева, не параллельна ни оси абсцисс, ни оси ординат.

Иногда Зевс хочет, чтобы Артемида вырубила для него деревья. Деревья должны быть вырублены так, чтобы выполнялись следующие условия:

  1. Зевс хочет, чтобы для него было вырублено хотя бы T деревьев.
  2. Чтобы потом построить прямоугольное футбольное поле для будущих футбольных успехов, Артемида должна вырубить все деревья внутри и на границе некоторой прямоугольной площадки, и ни одно дерево вне этой площадки.
  3. Стороны этой площадки должны быть параллельны осям координат.
  4. В двух противоположных углах площадки должны быть расположены деревья (которые будут вырублены).

Так как Артемида любит деревья, она хочет выполнить все условия таким образом, чтобы пришлось вырубить как можно меньше деревьев. Напишите программу, которая по информации о лесе и минимальному количеству деревьев T , которые должны быть вырублены, выбирает площадку, на которой Артемида будет вырубать деревья.

Входные данные

Первая строка ввода содержит единственное число N — количество деревьев в лесу ( 1 < N ≤ 20 000 ). Вторая строка содержит единственное число T — минимальное количество деревьев, которые должны быть вырублены ( 1 < T ≤ N ). Следующие N строк описывают расположение деревьев. Каждая из этих строк содержит по два целых числа X и Y — координаты дерева ( 0 ≤ X , Y ≤ 64 000 ). Решения, работающие только для N < 5000 , будут оцениваться из 50 баллов.

Выходные данные

Вывод должен содержать единственную строку, в которой записано два целых числа I и J , разделённых пробелом: Артемида должна вырубить деревья на площадке, углами которой будут деревья с номерами I и J (это те деревья, которые описаны в строках входного файла с номерами I + 2 и J + 2 ). Эти числа можно выводить в любом порядке. Возможно, есть несколько способов выбрать эти деревья, и в этом случае вы должны вывести любую из подходящих пар. Гарантируется, что во всех тестах жюри существует хотя бы одно решение.

Примеры
Входные данные
3
2
1 1
2 3
5 6
Выходные данные
1 2
#112528
Быстро растет бамбук...
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

Скоро начнётся сезон роста бамбука. Скупщики бамбука принимают любое количество бамбука каждый день ровно в полдень. Однако цена бамбука каждый день меняется. Нам удалось узнать, по какой цене скупщики будут принимать бамбук. Кроме того, мы точно знаем, на сколько метров вырастает бамбук за каждые сутки (эта величина тоже меняется). В любой день можно либо срезать весь бамбук целиком и продать его, либо оставить бамбук расти дальше. После срезания бамбук продолжает расти. Требуется определить, какую максимальную прибыль от продажи бамбука можно получить. В полдень нулевого дня (начало сезона роста бамбука) длина бамбука равна 0. Сезон роста бамбука длится ровно N суток.

Входные данные

В первой строке входного файла находится натуральное число N , 1 ≤ N ≤ 100000 . В каждой из следующих N строк содержатся два целых положительных числа, разделенных пробелом: цена одного метра бамбука в определенный день и на сколько метров вырос бамбук за последние сутки. В ( i + 1) - й строке файла содержатся данные, относящиеся к полудню i – го дня.

Выходные данные

В единственной строке выходного файла следует выводить одно целое неотрицательное число – наибольшая возможная выручка от продажи бамбука. Гарантируется, что результат не превосходит 2 63 - 1 .

Примеры
Входные данные
8
2 7
4 1
3 3
5 5
2 4
5 2
4 7
1 1
Выходные данные
139
Страница: << 294 295 296 297 298 299 300 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест