Числа в позиционной троично-симметричной системе счисления записываются с использованием трех символов: +, –, 0. Например, такими числами являются, например,

"+ + 0 – 0", "– – 0 +", "– – –".

Эти числа переводятся в десятичную систему как:

   а) + + 0 – 0 = 1*\(3^4\) + 1*\(3^3\) + 0*\(3^2\) – 1*\(3^1\) + 0*\(3^0\)

   б) – – 0 + = – 1*\(3^3\) – 1*\(3^2\) + 0*\(3^1\) + 1*\(3^0\)

   в) – – – = – 1*\(3^2\) – 1*\(3^1\) – 1*\(3^0\)

Над числами в позиционной троично-симметричной системе счисления можно выполнять два действия: сложение (+) и вычитание (–). Требуется написать программу, которая вычисляет сумму или разность чисел в троично-симметричной системе счисления. Таблица Пифагора для сложения цифр в троично-симметричной системе счисления имеет вид:

Дано прямоугольное поле, каждая клетка которого покрашена в какой-то цвет. За один ход необходимо перекрасить все клетки одного цвета в другой цвет. Стоимость перекраски одной клетки зависит от номера хода и задается функцией: \(F(i) = ((A \cdot F(i-1)+B) \bmod~C) + 1\), \(F_1\) – известная стоимость первого хода.

Необходимо за минимальное количество ходов перекрасить все поле в один цвет так, чтобы общая стоимость перекраски была бы максимальной.

Много в мире разных часовых поясов! Именно поэтому соревнования по программированию часто бывают в неудобное для некоторых людей время. Как-то раз Гриша и Егор решили поучавствовать в соревновании, которое заканчивалось очень поздно. Именно поэтому ребята решили переночевать в гостинице, чтобы не возвращаться домой поздно. Однако все не так просто. Родители Егора и Гриши очень волнуются за своих детей, поэтому они решили установить по всему городу камеры, чтобы видеть, где находятся ребята.

В городе, где живут программисты 1 ≤ n ≤ 500 000 перекрестков, соединенных n - 1 дорогой так, что между любыми двумя перекрестками существует путь по дорогам.

Родители собираются установить на перекрестках города камеры, радиус действия которых равен длине дороги. Родители будут спокойны, если смогут видеть ребят на любой дороге и на любом про перекрестке. Иными словами, для каждого перекрестка должен существовать перекресток, находящийся на расстоянии не более одной дороги, такой что на нем установлена камера и для любой дороги должна быть установлена камера хотя бы на одном конце этой дороги. Установка камер  — затратное дело, поэтому для каждого перекрестка с номером i известна стоимость 1 ≤ cost _i ≤ 10 ⁹ установки камеры на нем.

Помогите родителям установить камеры надлежащим образом за минимальную стоимость.

Телекоммуникационная сеть крупной IT-компании содержит n серверов, пронумерованных от 1 до \(n\). Некоторые пары серверов соединены двусторонними каналами связи, всего в сети m каналов. Гарантируется, что сеть серверов устроена таким образом, что по каналам связи можно передавать данные с любого сервера на любой другой сервер, возможно с использованием одного или нескольких промежуточных серверов.

Множество серверов \(A\) называется отказоустойчивым, если при недоступности любого канала связи выполнено следующее условие. Для любого не входящего в это множество сервера \(X\) существует способ передать данные по остальным каналам на сервер \(X\) хотя бы от одного сервера из множества \(A\).

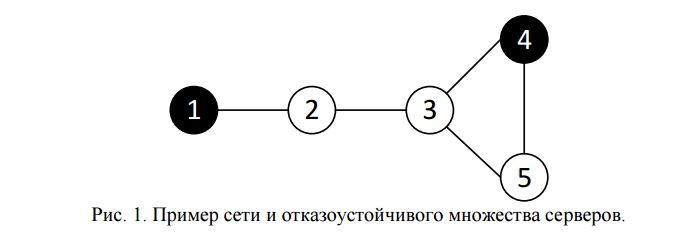
На рис. 1 показан пример сети и отказоустойчивого множества из серверов с номерами 1 и 4. Данные на сервер 2 можно передать следующим образом. При недоступности канала между серверами 1 и 2 — с сервера 4, при недоступности канала между серверами 2 и 3 — с сервера 1. На серверы 3 и 5 при недоступности любого канала связи можно по другим каналам передать данные с сервера 4.

В рамках проекта группе разработчиков компании необходимо разместить свои данные в сети. Для повышения доступности данных и устойчивости к авариям разработчики хотят продублировать свои данные, разместив их одновременно на нескольких серверах, образующих отказоустойчивое множество. Чтобы минимизировать издержки, необходимо выбрать минимальное по количеству серверов отказоустойчивое множество. Кроме того, чтобы узнать, насколько гибко устроена сеть, необходимо подсчитать количество способов выбора такого множества, и поскольку это количество способов может быть большим, необходимо найти остаток от деления этого количества способов на число \(10^9 + 7\).

Требуется написать программу, которая по заданному описанию сети определяет следующие числа: \(k\) — минимальное количество серверов в отказоустойчивом множестве серверов, \(c\) — остаток от деления количества способов выбора отказоустойчивого множества из \(k\) серверов на число \(10^9 + 7\)

Дано дерево из n вершин. У каждой вершины есть цвет. Нужно обработать q запросов ( v _i , c _i ): найти расстояние от v _i до ближайшей к v _i вершины цвета c _i . Расстоянием между вершинами называется минимальное количество рёбер в пути между ними.