В супермаркете «На троечку» часто происходят распродажи товаров, срок годности которых подходит к концу. Каждый товар привозят в магазин в определенное время, а через некоторое его вывозят из магазина, в связи с окончанием срока годности. Более формально, каждый товар имеет стоимость c _i , время его завоза в магазин a _i и время его вывоза из магазина b _i .

У Иннокентия есть хитрый план похода в магазин. Даже несколько. Каждый план похода в магазин выглядит так: Иннокентий выбирает какое-то время, когда он появится в магазине m _j , время s _j , которое он проведет в магазине среди огромных стеллажей товаров, и сумму денег k _j , которую он рассчитывает потратить. Для каждого плана он хочет узнать, сможет ли он осуществить его, т. е. верно ли, что он сможет во время своего пребывания в магазине купить несколько товаров суммарной стоимостью ровно k _j , при этом все выбранные товары должны быть в магазине на протяжении всего пребывания Иннокентия в магазине.

Помогите Иннокентию определить, какие из его планов можно выполнить.

Вася открыл для себя классическую игру «Bomberman», действующий лицом которой является Бомбермен. Этот персонаж передвигается по игровому полю, представляющему собой прямоугольник из N строк и M столбцов. Каждая клетка поля либо свободна для прохода, либо занята стеной. В одной из клеток находится бонус, к которому необходимо добраться Бомбермену. Для этого у него есть ровно 3 бомбы. За ход Бомбермен может сдвинуться в соседнюю клетку, если она свободна, или взорвать стену, расположенную в ней, использовав одну бомбу.

В последнем случае клетка становится проходимой и впоследствии Бомбермен может на нее встать. Вася хочет определить, за какое минимальное количество ходов Бомбермен сможет добраться до бонуса, или же узнать, что это сделать невозможно, тогда Вася может спокойно удалить «Bomberman» - а и вернуться к старой доброй Дотке.Соседними являются клетки, имеющие общую сторону. Бомбермен не может выходить за границы поля.

Вася очень любит учиться, но некоторые уроки в школе—полная скукотища. Для того чтобы скрасить время, они с Петей придумали игру. Перед началом партии ребята пишут на листочке два различных натуральных числа aиb . Затем по очереди делают ход: среди записанных чисел выбирают p и q такие, что модуля их разности | p − q | еще нет на листке, и дописывают его. Проигрывает тот, кто не может сделать ход. Определите, кто из ребят окажется победителем при правильной игре обоих. Вася вежливый мальчик, поэтому всегда ходит вторым.

На координатной плоскости вдоль оси OX, симметрично относительно начала координат, мирно расположился крейсер «Адмирал Василий». Крейсер расположен так, что его центр находится в точке (0, 0) , нос (передняя часть) — в точке (− L , 0) , а корма (задняя часть) — в точке ( L , 0) . Отнюдь не мирные цели визита «Адмирала Василия» на координатную плоскость выдают лишь две его установки ПВО, расположенные на носу и корме крейсера то есть в точках (− L , 0) и ( L , 0) .

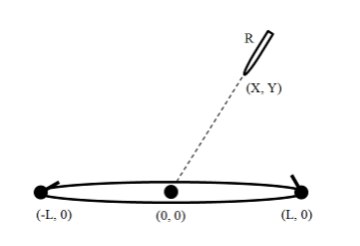
Хранители координатной плоскости не рады незваным гостям. С целью предотвращения потенциальной угрозы была выпущена ракета, направленная ровно в начало координат — центр крейсера. Ракета имеет длину R , на момент запуска нос ракеты находился в точке ( X , Y ) . Ракета расположена вдоль прямой, соединяющей нос ракеты и начало координат. Скорость полета ракеты — V (см.рисунок).

Как только ракета была запущена, её обнаружил крейсер и обе установки ПВО открыли огонь по ракете.

Установки ПВО работают следующим образом:

•они мгновенно поворачиваются, наводятся на нос ракеты и производят выстрел в этом направлении;

•скорость снаряда установки ПВО равна W ;

•установки ПВО продолжают стрелять до тех пор, пока ракета не будет уничтожена или пока крейсер не будет потоплен;

•первый выстрел установки ПВО производят в момент запуска ракеты, последующие выстрелы производятся с интервалом времени T , то есть между двумя выстрелами ракета пролетает расстояние V · T .

Если снаряд установки ПВО попадет в какую-то часть ракеты, то ракета будет уничтожена. При этом, если ракета достигнет носом центра крейсера, то , в свою очередь, крейсер будет потоплен. Какой минимальной скоростью W должны обладать снаряды установок ПВО, чтобы сбить ракету до того, как она уничтожит крейсер? Размерами снарядов установок ПВО, шириной крейсера и шириной ракеты можно пренебречь. Установки ПВО поворачиваются мгновенно. Первый выстрел они производят в момент запуска ракеты, а затем производят выстрелы с интервалом ровно T .

Королевские Железные Дороги (КЖД) готовятся открыть новый, скоростной, маршрут из столицы в соседний город NN и обратно. Новые поезда будут добираться до места назначения втрое быстрее обычных ночных поездов. Конкурс на поставку новых составов выиграла зарубежная компания «MacroHard» — производитель локомотивов «Hawk», которые будут использоваться в королевстве под локализованным названием «Ястреб». Расписание уже готово, но до сих пор не решен вопрос, сколько именно составов нужно, чтобы его выполнить. Не требуется покупать по составу на каждый рейс, поскольку поезд, прибывший на станцию, может выполнить и обратный рейс. КЖД обратились к вам и просят написать программу, способную рассчитать минимально необходимое количество поездов на один день. Расписание состоит из N ₁ рейсов из столицы в город NN и N ₂ обратных рейсов. Для каждого рейса известно время отправления и время прибытия — с точностью до минуты. Любой рейс полностью выполняется в течение одних календарных суток (с 00: 00 до 23: 59 включительно) — то есть никакой рейс не прибывает на следующий день после отправления. Каждый рейс занимает как минимум одну минуту, то есть ни один поезд не прибывает на станцию назначения в ту же минуту, в которую он отправился . КЖД настолько эффективны, что после прибытия поезд готов в ту же минуту отправиться в обратный рейс. Одновременно на станции может находиться, отправляться или прибывать любое количество поездов. Руководство КЖД не одобряет холостые поездки, поэтому поезда не могут перемещаться вне расписания в течение дня. Отметим, что вам не нужно учитывать подготовку к выполнению расписания следующего дня — к моменту начала следующих суток железнодорожники способны обеспечить любое распределение составов по станциям, независимо от того, как они были распределены к концу предыдущих.