У компании BigData Inc. есть
n
дата-центров, пронумерованных от
1
до
n
, расположенных по всему миру. В этих дата-центрах хранятся данные клиентов компании (как можно догадаться из названия — большие данные!)
Основой предлагаемых компанией BigData Inc. услуг является гарантия возможности работы с пользовательскими данными даже при условии выхода какого-либо из дата-центров компании из доступности. Подобная гарантия достигается путём использования
двойной репликации
данных. Двойная репликация — это подход, при котором любые данные хранятся в двух идентичных копиях в двух различных дата-центрах.
Про каждого из
m
клиентов компании известны номера двух различных дата-центров
c
i
, 1
и
c
i
, 2
, в которых хранятся его данные.
Для поддержания работоспособности дата-центра и безопасности данных программное обеспечение каждого дата-центра требует регулярного обновления. Релизный цикл в компании BigData Inc. составляет один день, то есть новая версия программного обеспечения выкладывается на каждый компьютер дата-центра каждый день.
Обновление дата-центра, состоящего из множества компьютеров, является сложной и длительной задачей, поэтому для каждого дата-центра выделен временной интервал длиной в час, в течение которого компьютеры дата-центра обновляются и, как следствие, могут быть недоступны. Будем считать, что в сутках
h
часов. Таким образом, для каждого дата-центра зафиксировано целое число
u
j
(
0 ≤
u
j
≤
h
- 1
), обозначающее номер часа в сутках, в течение которого
j
-й дата-центр недоступен в связи с плановым обновлением.
Из всего вышесказанного следует, что для любого клиента должны выполняться условия
u
c
i
, 1
≠
u
c
i
, 2
, так как иначе во время одновременного обновления обоих дата-центров, компания будет не в состоянии обеспечить клиенту доступ к его данным.
В связи с переводом часов в разных странах и городах мира, время обновления в некоторых дата-центрах может сдвинуться на один час вперёд. Для подготовки к непредвиденным ситуациям руководство компании хочет провести учения, в ходе которых будет выбрано некоторое непустое подмножество дата-центров, и время обновления каждого из них будет сдвинуто на один час позже внутри суток (то есть, если
u
j
=
h
- 1
, то новым часом обновления будет
0
, иначе новым часом обновления станет
u
j
+ 1
). При этом учения не должны нарушать гарантии доступности, то есть, после смены графика обновления должно по-прежнему выполняться условие, что данные любого клиента доступны хотя бы в одном экземпляре в любой час.
Учения — полезное мероприятие, но трудоёмкое и затратное, поэтому руководство компании обратилось к вам за помощью в определении минимального по размеру непустого подходящего подмножества дата-центров, чтобы провести учения только на этом подмножестве.
Выходные данные
В первой строке выведите минимальное количество дата-центров
k
(
1 ≤
k
≤
n
), которые должны затронуть учения, чтобы не потерять гарантию доступности. Во второй строке выведите
k
различных целых чисел — номера кластеров
x
1
,
x
2
, ...,
x
k
(
1 ≤
x
i
≤
n
), на которых в рамках учений обновления станут проводиться на час позже. Номера кластеров можно выводить в любом порядке.
Если возможных ответов несколько, разрешается вывести любой из них. Гарантируется, что хотя бы один ответ, удовлетворяющий условиям задачи, существует.
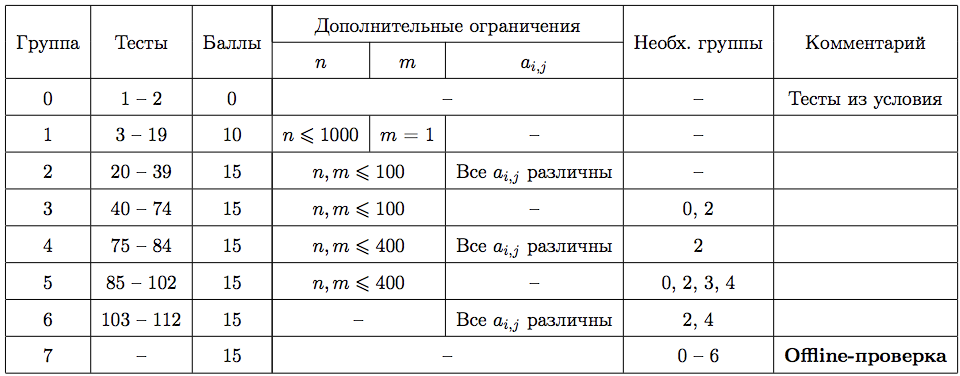
Система оценки
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при про- хождении всех тестов группы и всех тестов предыдущих групп.

Примечание
Рассмотрим первый тест из условия. Приведённый ответ является единственным способом провести учения, затронув только один дата-центр. В таком сценарии третий сервер начинает обновляться в первый час дня, и никакие два сервера, хранящие данные одного и того же пользователя, не обновляются в один и тот же час.
С другой стороны, например, сдвинуть только время обновления первого сервера на один час вперёд нельзя — в таком случае данные пользователей 1 и 3 будут недоступны в течение нулевого часа.
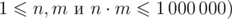 — количество строк и столбцов таблицы соответственно.
— количество строк и столбцов таблицы соответственно.