Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 323 324 325 326 327 328 329 >> Отображать по:
#114060
Кроссворд (Osmosmjerka)
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
256 megabytes

Мы создали бесконечный кроссворд, взяв прямоугольник размера \(\)\(N \times M\)\(\), заполненный буквами и замостили им бесконечную плоскость. Например, прямоугольник

honi

hsin

порождает следующий крссворд:
...honihonihonihoni...

...hsinhsinhsinhsin...

...honihonihonihoni...

...hsinhsinhsinhsin...

, который бесконечно продолжается во всех направлениях.

В данном кроссворде нами случайно (равновероятно) выбирается одна клетка и одно из восьми направлений. Затем начиная с данной клетки в данном направлении выписывается слово длины \(\)\(K\)\(\). Описанный процесс повторяется (независимо от первого раза) второй раз. Вам требуется вычислить вероятность того, что два выписанных слова совпадут.

Входные данные

Первая строка содержит три числа \(\)\(M, N, K\)\(\) (\(\)\(1 \leq N, M \leq 500\)\(\), \(\)\(1 \leq K \leq 10^9\)\(\)) — размеры блока и длина выбираемого слова соответственно.

Следующие \(\)\(M\)\(\) строк содержат по \(\)\(N\)\(\) латинских строчных букв, задавая блок, коим замощается доска. Гарантируется, что в данных есть хотя бы две различные буквы.

Выходные данные

Выведите требуемую вероятность в виде сокращённой дроби «p/q» без пробелов и кавычек.

Система оценки

Решение, правильно работающее на тестах, в которых \(\)\(N = M\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.

Примеры
Входные данные
1 2 2
ab
Выходные данные
5/16
Входные данные
2 4 3
honi
hsin
Выходные данные
19/512
Входные данные
3 3 10
ban
ana
nab
Выходные данные
2/27
#114061
Мухобойка (Meksikanac)
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.

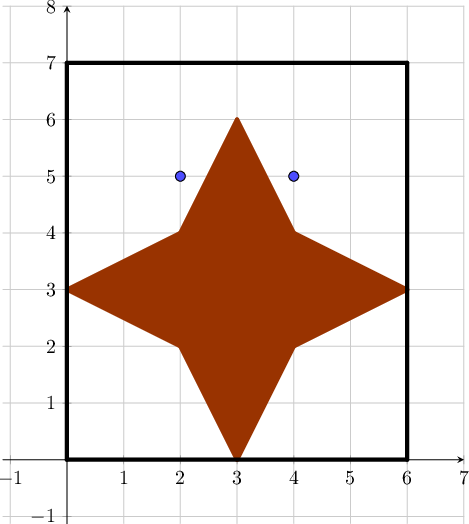
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.

Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.

Входные данные

Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.

Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)). 

В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\))  — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.

Выходные данные

Выведите искомое число способов ударить по окну, не задев ни одной мухи.

Система оценки

Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.

Примечание

Пояснение к третьему примеру:

Примеры
Входные данные
4 5 2
1 3
3 4
4
0 0
2 0
2 2
0 2
Выходные данные
4
Входные данные
5 5 3
1 4
1 3
2 2
3
4 7
6 3
7 6
Выходные данные
3
Входные данные
6 7 2
2 5
4 5
8
1 4
3 3
4 1
5 3
7 4
5 5
4 7
3 5
Выходные данные
1
#114089
Шарики
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Рассмотрим полоску из \(n\) клеточек. На каждой клетке написана какая-то буква латинского языка.

Также каждая клетка изначально содержит \(1\) шарик. Вы последовательно проделываете \(q\) операций следующего вида:

  • "\(c_i\) \(d_i\)" — сдвинуть все шарики, находящиеся в клетке с буквой \(c_i\) в сторону \(d_i\) (\(d_i\) равно или "R" или "L")

Все шарики сдвигаются одновременно. Если какой-то шарик пытается сдвинутся налево из клетки номер \(1\) или направо из клетки \(n\), то он исчезает. Выясните сколько всего останется шариков после выполнения всех операций.

Входные данные

Первая строка содержит целые числа \(n\) и \(q\) (\(1 \le n, q \le 200\,000\)) — длину полоски и количество операций. Следующая строка содержит строку \(s\) длины \(n\), состоящую только из заглавных букв латинского алфавита и задающую буквы в каждой клетке полоски. Оставшиеся \(q\) строк задают операции в виде

  • "\(c_i\) \(d_i\)" — где \(c_i\) является заглавной буквой латинского алфавита, а \(d_i\) или "L", или "R"

Выходные данные

Выведите одно число — количество оставшихся шариков.

Примеры
Входные данные
4 3
BADB
B R
A L
B L
Выходные данные
1
#114090
ПСП
  

Правильные скобочные последовательности определяются следующим образом:

  • Пустая скобочная последовательность — правильная.
  • Если \(S\) — правильная скобочная последовательность, то \((S)\) тоже является правильной.
  • Если \(S_1\) и \(S_2\) — правильные скобочные последовательности, то \(S_1 S_2\) тоже является правильной.

Зная число \(n\), выведите все правильные скобочные последовательности длины \(2n\) в лексикографическом порядке. Символ '(' считается меньше символа ')'.

Входные данные

Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 12\)).

Выходные данные

Выведите все правильные скобочные последовательности в лексикографическом порядке.

#114091
Топологическая сортировка
  

Задан ориентированный ациклический граф с \(n\) вершинами и \(m\) ребрами. Также задана перестановка вершин графа. Необходимо проверить, является ли данная перестановка топологической сортировкой.

Входные данные

В первой строке даны два числа \(n\) и \(m\) — количество вершин и ребер в графе соответственно (\(1 \leq n, m \leq 10^5\)). В следующих \(m\) строках заданы пары чисел \(u_i, v_i\), означающие, что в графе есть ребро из вершины \(u_i\) в вершину \(v_i\). В последней строке задана перестановка из \(n\) элементов.

Выходные данные

Выведите "YES" (без кавычек), если данная перестановка является топологической сортировкой и "NO" в противном случае.

Примеры
Входные данные
3 3
2 3
1 3
1 2
2 1 3
Выходные данные
NO
Входные данные
3 3
3 2
1 2
3 1
3 1 2
Выходные данные
YES
Страница: << 323 324 325 326 327 328 329 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест