Страница: << 324 325 326 327 328 329 330 >> Отображать по:

#114092

Необычная яблоня

Темы: [Обход в глубину] [Деревья]

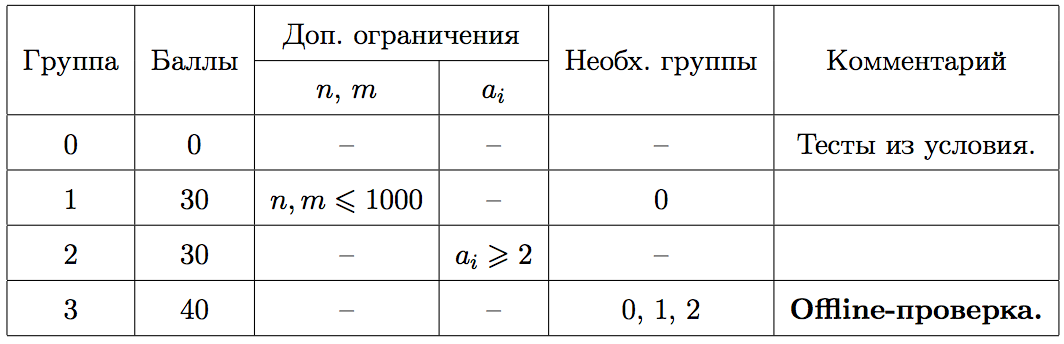
У Аркадия в саду есть одна необычная яблоня, с которой иногда необходимо собирать яблоки. Так как яблоня необычная, на ней есть $n$ соцветий, они пронумерованы от 1 до $n$. Соцветие номер 1 находится около корня дерева, любое другое соцветие с номером $i(i>1)$ расположено на верхнем конце ветки, нижний конец которой расположен в соцветии $p_i$.

Когда яблоки созревают, одновременно появляется ровно по одному яблоку в каждом соцветии. В тот же момент все яблоки начинают скатываться вниз по веткам к корню дерева. Каждую секунду все яблоки, кроме находящегося в первом соцветии, одновременно скатываются на одну ветку ближе к корню, то есть, например, из соцветия a яблоко попадет в соцветие $p_a$. Яблоки, находившиеся в первом соцветии, забирает Аркадий. Яблоня необычная, поэтому, если в какой-то момент в одном соцветии оказываются два яблока, они аннигилируют. Так происходит с каждой парой, например, если в соцветие попадет одновременно 5 яблок, то останется только одно яблоко, а если в соцветие попадет одновременно 8 яблок, то не останется ни одного яблока. Таким образом, в каждом соцветии в любой момент времени находится не более одного яблока.

Помогите Аркадию, подсчитайте, сколько яблок он сможет забрать из первого соцветия за один урожай.

Входные данные

В первой строке следует целое число $n(2 \le n \le 100000)$ — количество соцветий.

Во второй строке следует последовательность целых чисел $p_2, p_3, ..., p_n$, состоящая из $n−1$ числа, где $p_i$ равно номеру соцветия, в которое скатывается яблоко из соцветия $i$.

Выходные данные

Выведите количество яблок, которые Аркадий сможет забрать из первого соцветия за один урожай.

Примеры

Входные данные

3
1 2

Выходные данные

Входные данные

5
4 2 5 1

Выходные данные

#114114

Вложенные коробки с конфетами

Темы: [Бинарный поиск]

В качестве новогоднего подарка Андрей получил коробку с конфетами. Или не совсем коробку. На самом деле он быстро обнаружил, что внутри коробки находятся ещё несколько одинаковых коробок меньшего размера, внутри которых содержатся ещё меньшие коробки и так далее... Формально, скажем что конфета является коробкой уровня 0 , а коробка уровня i содержит в себе a _i коробок уровня i - 1 . Коробка, подаренная Андрею, имеет уровень n .

Сегодня к Андрею в гости придут друзья и он хочет поделиться с ними некоторым количеством конфет, для чего ему придётся открыть некоторое количество коробок. Разумеется, Андрей не может открыть коробку, если она находится внутри ещё не открытой коробки. Ему хотелось бы знать, какое минимальное количество коробок ему потребуется открыть, чтобы достать x конфет. Поскольку Андрей ещё не уверен, сколько друзей к нему сегодня придут, он просит вас решить задачу для нескольких значений x .

Входные данные

В первой строке входных данных записаны числа n и m ( 1 ≤ n , m ≤ 300 000 ) — количество коробок и количество вопросов Андрея соответственно.

Во второй строке записаны n целых чисел a ₁ , a ₂ , ..., a _n ( 1 ≤ a _i ≤ 10 ⁹ ).

В третьей строке записаны m чисел x ₁ , x ₂ ..., x _m ( 1 ≤ x _i ≤ 10 ¹² ) — значения количества конфет, для которых Андрей хочет знать ответ. Гарантируется, что каждое значение x _i не превосходит общего число конфет в коробке уровня n .

Выходные данные

Выведите m целых чисел, i -е из них должно равняться минимальному количеству коробок, которое потребуется открыть Андрею, чтобы получить хотя бы x _i конфет.

Система оценки

Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп, указанных в таблице ниже.

$\text{[math]}$

Примечание

В первом примере единственная конфета спрятана в пяти уровнях коробок.

Во втором примере, чтобы получить 13 конфет, Андрей должен открыть самую большую коробку, затем две коробки уровня 2 , и, наконец, пять из шести имеющихся коробок уровня 1 .

Примеры

Входные данные

5 1
1 1 1 1 1
1

Выходные данные

Входные данные

3 3
3 3 3
2 8 13

Выходные данные

3
5
8

#114304

Расстояние

Темы: [Арифметические алгоритмы]

Рассмотрим следующую операцию, определённую на целых положительных числах. Операция состоит в умножении числа $q$ на простое число $p$, либо в делении числа $q$ на простое число $p$, если $q$ делится на $p$ без остатка. Назовем расстоянием между числами $a$ и $b$ минимальное количество операций, необходимое для того чтобы получить из числа $a$ число $b$. Обозначим расстояние как $d(a, b)$.

Дана последовательность из $n$ положительных чисел $a_1, a_2, ... a_n$. Для каждого индекса $i$ ($ 1 \le i \le n$) необходимо найти индекс $j$, такой что $1 \le j \le n$ и $i \ne j$, и что $d(a_i, a_j)$ минимально.

Входные данные

Первая строка входных данных содержит одно целое число $n$ — количество элементов в последовательности $a$ ($1 \le n \le 100 000$).

В последующих $n$ строках входных данных даны $n$ целых чисел $a_1, a_2, \ldots, a_n$ — элементы последовательности ($1 \le a_i \le 10^{6}$) ($i$-е число в $i + 1$ строке).

Выходные данные

Выведете $n$ строк. В $i$ строке выведете такой минимальный индекс $j$, такой что $1 \le j \le n$ и $i \ne j$, и что $d(a_i, a_j)$ минимально.

Система оценки

В тестах суммарной стоимостью не менее $30$ баллов дополнительно гарантируется что $n \le 1000$, $a_i \le 10000$.

Примеры

Входные данные

Выходные данные

Входные данные

2
1
1

Выходные данные

2
1

#114305

Телепортация_0

Темы: [Алгоритмы на графах] [Обход в ширину]

На дворе $3020$ год. Король Байтазар правит огромной планетарной системой, в которой насчитывается целых $n$ планет. В $3020$ году люди отказались от традиции давать планетам имена и вместо этого используют номера. Дворец Байтазара находится на планете под номером $1$, в то время как его военная база находится на планете под номером $2$. Давным давно для Байтазара был построен портал, соединяющий планеты $1$ и $2$, который позволяет добираться с планеты номер $1$ на планету номер $2$ или обратно за $250$ минут (немногим больше четырёх часов).

С тех пор технологии шагнули далеко вперёд, и современные порталы позволяют добиратся между планетам всего за $1$ час (в $3020$ году в часе всё ещё $60$ минут). Порталы, разумеется, остались двухсторонними. Некоторые из планет уже соединены современными версиями порталов (но не планеты $1$ и $2$ - король Байтазар крайне консервативен). Вообще, уже сейчас возможно добраться от планеты $1$ до планеты $2$ используя имеющиеся новые порталы, но личный портал Байтазара остаётся самым быстрым способом добраться между планетами $1$ и $2$.

Технология быстрой телепортации продолжает своё распространение и Байтазар хочет это поддержать, не желая между тем менять свой личный портал старого типа на новый. При этом, из соображений безопасности Байтазар не хочет, чтобы был способ добраться с планеты $1$ на планету $2$ быстрее, чем его личный портал. Помогите Байтазару. Найдите максимальное число новых порталов, которые можно построить так, чтобы личный портал Байтазара оставался самым быстрым путем перемещения между резиденцией и военной базой.

Входные данные

В первой строке даны два числа $n$ и $m$ ($ 2 \le n \le 40000, 1 \le m \le 1000000$) - количество планет в планетарной системе Байтазара и количество двусторонних порталов нового типа соответственно.

В последующих $m$ строках дано описания порталов. Каждая строка содержит два целых числа $v$ и $u$, ($1 \le v, u \le n$, $v \ne u$), что означает что планеты $v$ и $u$ соединены порталом нового типа.

Гарантируется, что существует способ добраться с планеты $1$ на планету $2$ используя имеющиеся порталы и что такое путешествие займёт строго больше $250$ минут.

Выходные данные

Выведете единственное число $ans$ - наибольшее количество порталов которое можно построить в планетарной системы Байтазара, так чтобы личный портал Байтазара оставался самым быстрым путем перемещения между резиденцией и военной базой.

Система оценки

В тестах суммарной стоимостью не менее $20$ баллов дополнительно гарантируется что $n \le 8$, $m \le 9$.

В тестах суммарной стоимостью не менее $30$ баллов дополнительно гарантируется что $n \le 12$, $m \le 20$.

В тестах суммарной стоимостью не менее $60$ баллов дополнительно гарантируется что $n \le 150$, $m \le 4000$.

Примечание

Иллюстрация к первому примеру:

$\text{[math]}$

Жирными линиями показаны имеющиеся скоростные порталы, в то время как пунктирными линиями показаны те порталы, которые Байтазар может построить, не подвергнув государство опасности и построив при этом максимально возможное количество скоростных порталов.

Примеры

Входные данные

Выходные данные

#114306

Префиксуффикс

Темы: [Алгоритмы на строках] [Z-функция, Префикс-функция]

Строка $s$ назывется префиксом строки $t$, если строка $t$ начинается со строки $s$. Строка $s$ назывется суффиксом строки $t$, если строка $t$ заканчивается на строку $s$.

Назовём две строки $s$ и $t$ циклически эквивалентными, если существует циклический сдвиг, переводящий строку $s$ в строку $t$; другими словами строки $s$ и $t$ циклически эквивалентны тогда и только тогда, когда, строка $s$ может быть получена из строки $t$ путем перемещения некого суффикса строки $t$ в начало строки $t$. Например, строки $ababba$ и $abbaab$ циклически эквивалентны, в то время как строки $ababba$ и $ababab$ нет. В частности, любая строка циклически эквивалентна самой себе.

Дана строка $t$ длины $n$. Требуется найти такой префикс $p$ и такой суффикс $s$ строки $t$, что:

$p$ циклически эквивалентен $s$ (и, как следствие, их длины равны)
длина $p$ не превосходит $\frac{n}{2}$ (то есть $p$ и $s$ не пересекаются в $t$)
длина $p$ максимальна

Входные данные

Первая строка входных данных содержит одно целое число $n$ — длину строки $е$ ($1 \le n \le 1000 000$).

Вторая строка входных данных содержит строку $t$ состоящую из строчных латинких букв.

Выходные данные

Выведите единственное целое число $res$ - наибольшее целое число, такое что ($0 \le res \le \frac{n}{2}$) и $res$ - ый префикс строки $t$ циклически эквивалентен $res$-му суффиксу строки $t$.

Система оценки

В тестах суммарной стоимостью не менее $30$ баллов дополнительно гарантируется что $n \le 500$.

В тестах суммарной стоимостью не менее $50$ баллов дополнительно гарантируется что $n \le 5000$.

В тестах суммарной стоимостью не менее $80$ баллов дополнительно гарантируется что $n \le 200000$.

В тестах суммарной стоимостью не менее $90$ баллов дополнительно гарантируется что $n \le 500000$.

Примеры

Входные данные

15
ababbabababbaab

Выходные данные

Страница: << 324 325 326 327 328 329 330 >> Отображать по:

Выбрано

Отменить

Добавить в контест