Сортировка записей(9 задач)
Использование сортировки(13 задач)
Быстрая сортировка(55 задач)
Сортировка слиянием(9 задач)
Сортировка подсчетом(27 задач)
Сканирующая прямая(39 задач)
Сортировка событий(4 задач)
Рассмотрим строку \(s\), состоящую из строчных букв латинского алфавита. Примером такой строки является, например, строка «abba».
Подстрокой строки \(s\) называется строка, составленная из одного или нескольких подряд идущих символов строки \(s\). Обозначим как \(W(s)\) множество, состоящее из всех возможных подстрок строки \(s\). При этом каждая подстрока входит в это множество не более одного раза, даже если она встречается в строке \(s\) несколько раз.
Например, \(W\)(«abba») = {«a», «b», «ab», «ba», «bb», «abb», «bba», «abba»}.
Подпоследовательностью строки \(s\) называется строка, которую можно получить из \(s\) удалением произвольного числа символов. Обозначим как \(Y\)(\(s\)) множество, состоящее из всех возможных подпоследовательностей строки \(s\). Аналогично \(W\)(\(s\)), каждая подпоследовательность строки \(s\) включается в \(Y\)(\(s\)) ровно один раз, даже если она может быть получена несколькими способами удаления символов из строки \(s\). Поскольку любая подстрока строки \(s\) является также ее подпоследовательностью, то множество \(Y\)(\(s\)) включает в себя \(W\)(\(s\)), но может содержать также и другие строки.
Например, \(Y\)(«abba») = \(W\)(«abba») ∪ {«aa», «aba»}. Знак ∪ обозначает объединение множеств.
Будем называть строку \(s\) странной, если для нее \(W\)(\(s\)) = \(Y\)(\(s\)). Так, строка «abba» не является странной, а, например, строка «abb» является, так как для нее \(W\)(«abb») = \(Y\)(«abb») = {«a», «b», «ab», «bb», «abb»}.
Будем называть странностью строки число ее различных странных подстрок. При вычислении странности подстрока считается один раз, даже если она встречается в строке \(s\) в качестве подстроки несколько раз. Так, для строки «abba» ее странность равна 7, любая ее подстрока, кроме всей строки, является странной.
Требуется написать программу, которая по заданной строке \(s\) определяет ее странность.
Входной файл содержит строку \(s\), состоящую из строчных букв латинского алфавита. Строка имеет длину от 1 до 200 000.
Выходной файл должен содержать одно целое число: странность заданной во входном файле строки.
В этой задаче четыре подзадачи. Баллы за каждую подзадачу начисляются только в случае, если все тесты для данной подзадачи успешно пройдены.
Строка \(s\) состоит только из букв «a» и «b». Длина строки \(s\) не превышает 50.
Длина строки \(s\) не превышает 50.
Длина строки \(s\) не превышает 1000.
Длина строки \(s\) не превышает 200 000.
abba
7
Андрей работает судьей на чемпионате по гипершашкам. В каждой игре в гипершашки участвует три игрока. По ходу игры каждый из игроков набирает некоторое положительное целое число баллов. Если после окончания игры первый игрок набрал \(a\) баллов, второй — \(b\), а третий \(c\), то говорят, что игра закончилась со счетом \(a:b:c\).
Андрей знает, что правила игры гипершашек устроены таким образом, что в результате игры баллы любых двух игроков различаются не более чем в \(k\) раз.
После матча Андрей показывает его результат, размещая три карточки с очками игроков на специальном табло. Для этого у него есть набор из n карточек, на которых написаны числа \(x_1, x_2, …, x_n\). Чтобы выяснить, насколько он готов к чемпионату, Андрей хочет понять, сколько различных вариантов счета он сможет показать на табло, используя имеющиеся карточки.
Требуется написать программу, которая по числу \(k\) и значениям чисел на карточках, которые имеются у Андрея, определяет количество различных вариантов счета, которые Андрей может показать на табло.
Первая строка входного файла содержит два целых числа: \(n\) и \(k (3 \le n \le 100 000, 1 \le k \le 10^9\) ).
Вторая строка входного файла содержит \(n\) целых чисел \(x_1, x_2, …, x_n (1 \le x_i \le 10^9 )\).
Выходной файл должен содержать одно целое число — искомое количество различных вариантов счета.
В приведенном примере Андрей сможет показать следующие варианты счета: 1:1:2, 1:2:1, 2:1:1, 1:2:2, 2:1:2, 2:2:1, 2:2:3, 2:3:2, 3:2:2. Другие тройки чисел, которые можно составить с использованием имеющихся карточек, не удовлетворяют заданному условию, что баллы любых двух игроков различаются не более чем в \(k\) = 2 раза.
В этой задаче четыре подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи пройдены.
\(3 \le n \le 100 000, k = 1, 1 \le x_i \le 100 000\)
\(3 \le n \le 100, k \le 100, 1 \le x_i \le 100\)
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\), все \(x_i\) различны
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\)
5 2 1 1 2 2 3
9
Прямоугольная детская площадка полностью замощена \(N\) плитками. Все плитки прямоугольные, возможно разного размера. Плитки не перекрываются.
На этой площадке решили построить песочницу. Чтобы подготовить место для песочницы, необходимо вынуть не более K плиток таким образом, чтобы песочница занимала все освободившееся пространство, была прямоугольной и имела максимально возможную площадь.
Напишите программу, которая определяет расположение песочницы, удовлетворяющей перечисленным выше требованиям.
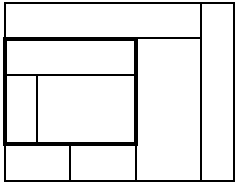
Введем систему координат так, чтобы начало координат совпадало с одним из углов площадки, а оси координат шли вдоль сторон площадки. В этом случае противоположный угол площадки окажется в точке \((X,Y)\).
Первая строка содержит два числа \(X\) и \(Y\) (натуральные числа, не превышающие 10000). Во второй строке заданы числа \(N\) и \(K (1 \le K \le N \le 2000)\). Следующие \(N\) строк файла содержат по четыре целых числа \(X_{i,1}, Y_{i,1}, X_{i,2}, Y_{i,2}\), задающих координаты двух противоположных углов плитки.
Выведите координаты двух противоположных углов найденного прямоугольника. Если решений несколько, выведите любое из них.
В этой задаче 16 тестов, каждый тест оценивается независимо.
Гарантируется, что решения, корректно работающие при \(n \le 25\) наберут не менее 30 баллов.
Гарантируется, что решения, корректно работающие при \(n \le 500\) наберут не менее 42 баллов.
Гарантируется, что решения, корректно работающие при \(n \le 1500\) наберут не менее 54 баллов.
7 5 8 3 0 0 2 1 2 0 4 1 0 1 1 3 1 1 4 3 0 3 4 4 0 4 6 5 4 0 6 4 6 0 7 5
0 1 4 4
Дано прямоугольное поле, каждая клетка которого покрашена в какой-то цвет. За один ход необходимо перекрасить все клетки одного цвета в другой цвет. Стоимость перекраски одной клетки зависит от номера хода и задается функцией: \(F(i) = ((A \cdot F(i-1)+B) \bmod~C) + 1\), \(F_1\) – известная стоимость первого хода.
Необходимо за минимальное количество ходов перекрасить все поле в один цвет так, чтобы общая стоимость перекраски была бы максимальной.
В первой строке натуральные задаются числа \(F_1\), \(A\), \(B\) и \(C\) (\(1 \leq F_1, A, B, C \leq 10000\)) – параметры функции \(F\). Во второй строке задаются два натуральных числа \(M\) и \(N\) (\(1 \leq N, M \leq 50\)) – размеры поля. В последующих \(M\) строках записано по \(N\) натуральных чисел, не превосходящих \(2^{31}\) – цвета клеток.
В первую строку выведите минимальное число ходов. Во вторую строку выведите в каком порядке будут перекрашиваться цвета, встречающиеся в таблице.
60 баллов ставится за решения, работающие на тестах, в которых номер цвета не превосходит \(10^5\).
В супермаркете «На троечку» часто происходят распродажи товаров, срок годности которых подходит к концу. Каждый товар привозят в магазин в определенное время, а через некоторое его вывозят из магазина, в связи с окончанием срока годности. Более формально, каждый товар имеет стоимость c i , время его завоза в магазин a i и время его вывоза из магазина b i .
У Иннокентия есть хитрый план похода в магазин. Даже несколько. Каждый план похода в магазин выглядит так: Иннокентий выбирает какое-то время, когда он появится в магазине m j , время s j , которое он проведет в магазине среди огромных стеллажей товаров, и сумму денег k j , которую он рассчитывает потратить. Для каждого плана он хочет узнать, сможет ли он осуществить его, т. е. верно ли, что он сможет во время своего пребывания в магазине купить несколько товаров суммарной стоимостью ровно k j , при этом все выбранные товары должны быть в магазине на протяжении всего пребывания Иннокентия в магазине.
Помогите Иннокентию определить, какие из его планов можно выполнить.
В первой строке входных данных содержится число N — общее количество товаров в магазине ( 1 ≤ N ≤ 500 ). Далее содержатся описания товаров, каждый товар описывается тремя целыми числами c i , a i , b i , обозначающими стоимость товара, время его завоза и время его вывоза из магазина ( 1 ≤ c i ≤ 1 000 , 1 ≤ a i < b i ≤ 10 9 ).
Далее содержится число M — количество планов Иннокентия ( 1 ≤ M ≤ 500 000 ). Каждый план описывается тремя целыми числами m j , k j , s j , обозначающими время прихода Иннокентия в магазин, сумму денег, которую он готов потратить в этом плане и длительность его пребывания в магазине ( 1 ≤ m j ≤ 10 9 , 1 ≤ k j ≤ 100 000 , 0 ≤ s j ≤ 10 9 ).
Помните, что это только планы, т. е. ситуация в магазине не меняется вне зависимости от того, может ли Иннокентий осуществить план или нет.
Для каждого плана в отдельной строке выведите « YES », если Иннокентий может его осуществить, и « NO » в противном случае.
Тесты к этой задаче состоят из четырех групп.
Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы.
5 6 2 7 5 4 9 1 2 4 2 5 8 1 3 9 5 2 7 1 2 7 2 3 2 0 5 7 2 4 1 5
YES NO YES YES NO