Стек(35 задач)
Дек(6 задач)
Список(7 задач)
Префиксные суммы(минимумы, ...)(2 задач)
Гоблины Мглистых гор очень любях ходить к своим шаманам. Так как гоблинов много, к шаманам часто образуются очень длинные очереди. А поскольку много гоблинов в одном месте быстро образуют шумную толку, которая мешает шаманам проводить сложные медицинские манипуляции, последние решили установить некоторые правила касательно порядка в очереди.
Обычные гоблины при посещении шаманов должны вставать в конец очереди. Привилегированные же гоблины, знающие особый пароль, встают ровно в ее середину, причем при нечетной длине очереди они встают сразу за центром.
Так как гоблины также широко известны своим непочтительным отношением ко всяческим правилам и законам, шаманы попросили вас написать программу, которая бы отслеживала порядок гоблинов в очереди.
В первой строке входных данный записано число \(N\) (\(1\le N\le 10^5\)) - количество запросов к программе. Следующие \(N\) строк содержат описание запросов в формате:
Для каждого запроса типа "-" программа должна вывести номер гоблина, который должен зайти к шаманам.
7 + 1 + 2 - + 3 + 4 - -
1 2 3
Для моделирования различных объектов часто применяются так называемые клеточные поля. В простейшем случае – это прямоугольные таблицы, характеризующие некоторую область, а в каждой ячейке таблицы записывается какая-либо информация об исследуемом объекте. В биологии для моделирования распространения вирусов на плоской области в каждой ячейке помечается наличие вируса, а его распространение осуществляется в соседние ячейки по вертикали и горизонтали за одну единицу времени. Некоторые клетки обладают иммунитетом, заразить их невозможно и через них не распространяются вирусы.
Требуется написать программу, которая определяет минимально возможное число вирусов, с помощью которых можно заразить всю исследуемую прямоугольную область (за исключением защищённых клеток).
В приведённом примере таблица имеет размер \(4\times5\), в ней символом "I" помечены защищённые клетки. Видно, что двух вирусов достаточно для заражения всей области. Их можно поместить, например, в клетки, помеченные символом "V".

В первой входной строке записаны два натуральных числа \(M\) и \(N\) - размеры таблицы (количество строк и столбцов соответственно). Известно, что
\(1 \le M, N \le 100\). Во второй строке вначале записано одно число \(K\) - количество защищённых клеток, а далее записаны \(2K\) чисел – координаты этих клеток \(x_i\), \(y_i\) (\(0 \le k \le M \times N, 1 \le x_i \le M, 1 \le y_i \le N\)).
Программа должна вывести одно число – минимально возможное число вирусов.
4 5 3 1 3 2 1 2 2
2
Школьники готовятся к участию в соревновании по программированию квадрокоптеров. Квадрокоптер, который используется в соревновании, может выполнять две команды: подняться вверх на 1 метр и опуститься вниз на 1 метр. Команда подъёма обозначается символом «(», а команда спуска — символом «)».
Программа для квадрокоптера представляет собой последовательность команд. Программа считается корректной, если, начав её исполнение на уровне земли и выполнив последовательно все команды, квадрокоптер снова оказывается на уровне земли. При этом в процессе выполнения программы квадрокоптер не должен пытаться опуститься ниже уровня земли.
Например, следующие программы являются корректными: «()(())», «((()))». Программа«(((» не является корректной, поскольку квадрокоптер завершает ее выполнение на высоте 3 метра над уровнем земли, программа «())(» также не является корректной, поскольку при выполнении третьей команды квадрокоптер пытается опуститься ниже уровня земли.
Участник соревнования написал корректную программу для квадрокоптера, состоящую из n команд, пронумерованных от 1 до n. Он загрузил её в память квадрокоптера для демонстрации во время соревнования. К сожалению, после загрузки программы в память квадрокоптера участник случайно удалил её на своём компьютере, а квадрокоптер не позволяет выгрузить программу из своей памяти.
К счастью, квадрокоптер поддерживает специальный режим отладки программы. В этом режиме квадрокоптер с загруженной в него программой может отвечать на специальные запросы. Каждый запрос представляет собой два целых числа: l и r, 1 ≤ l ≤ r ≤ n. В ответ на запрос квадрокоптер сообщает, является ли фрагмент загруженной в него программы, состоящий из команд с l-й по r-ю включительно, корректной программой для квадрокоптера, либо нет. Участник хочет с помощью режима отладки восстановить загруженную в квадрокоптер программу.
Требуется написать программу-решение, которая взаимодействует с программой жюри, моделирующей режим отладки квадрокоптера, и в итоге восстанавливает загруженную в квадрокоптер программу.
Это интерактивная задача.
Сначала на вход подаётся целое число n — количество команд в программе квадрокоптера (2 ≤ n ≤ 50 000).
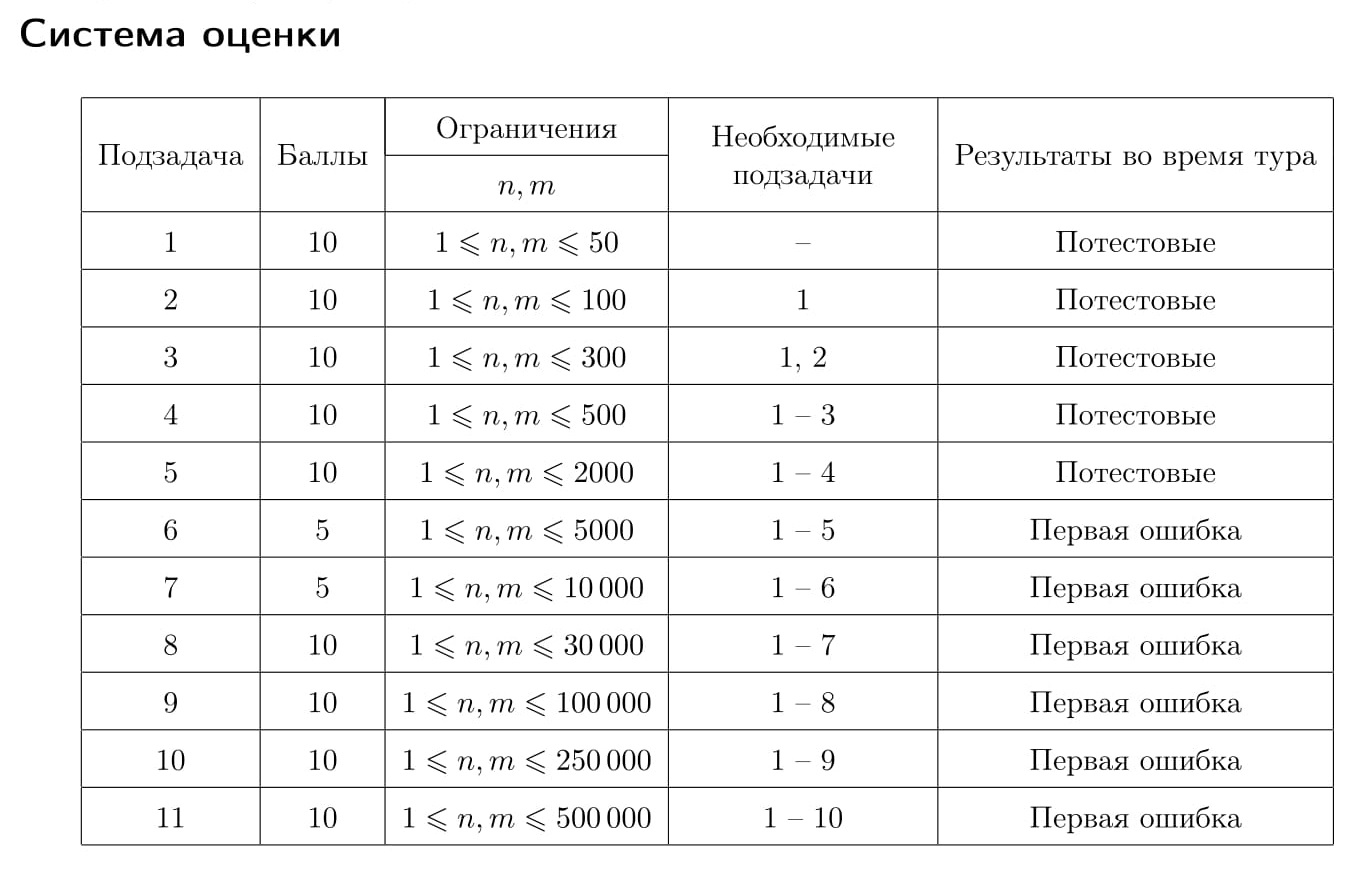
Для каждого теста жюри зафиксировано число k — максимальное количество запросов. Гарантируется, что k запросов достаточно, чтобы решить задачу. Это число не сообщается программе-решению. Ограничения k в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов к программе жюри, то на этом тесте она получает в качестве результата тестирования «Неверный ответ».
Чтобы сделать запрос, программа-решение должна вывести строку вида «? l r», где l и r — целые положительные числа, задающие фрагмент программы квадрокоптера (1 ≤ l ≤ r ≤ n).
В ответ на запрос программы-решения программа жюри подаёт ей на вход либо строку «Yes», либо строку «No», в зависимости от того, является ли запрошенный фрагмент программы квадрокоптера корректной программой.
Если программа-решение определила ответ на задачу, то она должна вывести строку «! c1c2... cn», где символ ci задаёт i-ю команду в программе квадрокоптера и равен либо «(», либо «)».
После этого программа-решение должна завершиться.
Гарантируется, что в каждом тесте программа в памяти квадрокоптера является фиксированной корректной программой, которая не меняется в зависимости от запросов, произведённых программой-решением.

Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.
В первом примере n = 4. Единственная возможная корректная программа из двух команд это «()», поэтому из результатов третьего и четвёртого запросов можно сделать вывод, что программа в памяти квадрокоптера — «()()». Поэтому, в частности, ответ на второй запрос действительно «No», так как фрагмент программы «()(» не является корректной программой: если квадрокоптер исполнит именно эти три команды, он останется на уровне одного метра над землёй.
В втором примере n = 6, и произведённых запросов достаточно, чтобы однозначно определить, что программа в памяти квадрокоптера — «((()))».
В тестах из условия k = 150, то есть, разрешается произвести не более 150 запросов.

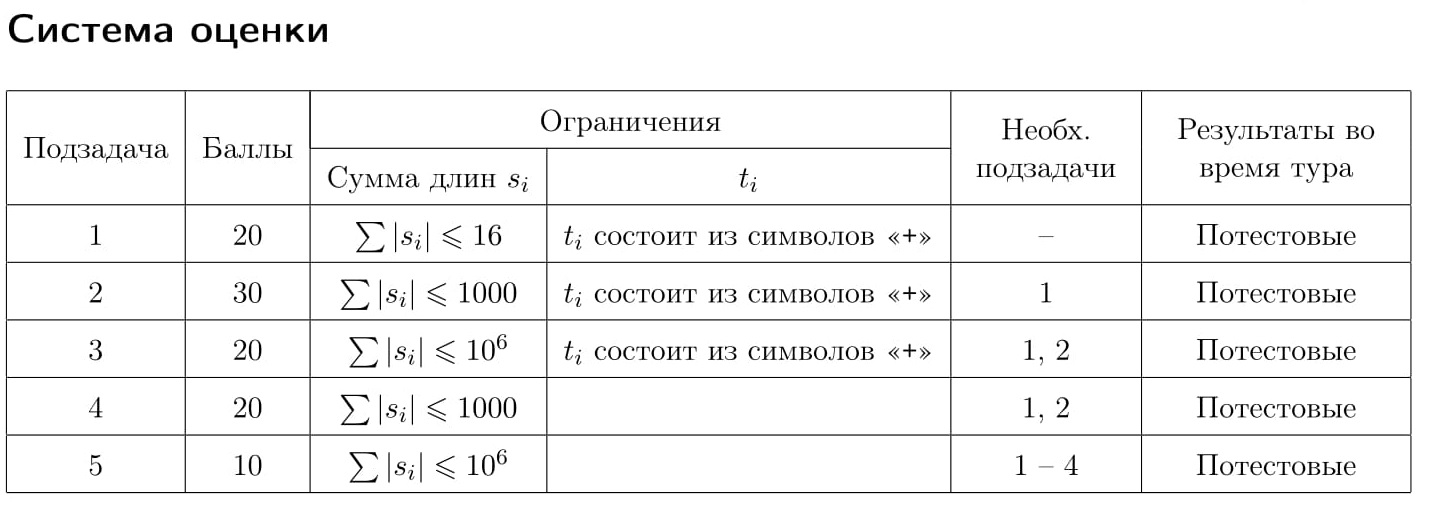
Исследуется новое цифровое устройство для хранения информации. Информация на устройстве хранится в виде последовательности ячеек, каждая из которых находится в одном из двух состояний, обозначаемых символами «+» и «-», и, таким образом, хранит один бит информации.
Назовём фрагментом группу соседних ячеек с одинаковым состоянием, слева от которой либо нет ячеек, либо находится ячейка в противоположном состоянии, и справа — либо нет ячеек, либо находится ячейка в противоположном состоянии.
Операция записи позволяет выбрать любую пару соседних фрагментов разной длины и изменить состояние всех ячеек более короткого фрагмента на противоположное, объединяя таким образом два или три соседних фрагмента в один.
Требуется написать программу, которая по заданной исходной и итоговой последовательностям состояний ячеек определяет, можно ли из исходной последовательности получить итоговую с помощью последовательных операций записи.
Первая строка входных данных содержит целое положительное число q — количество тестов.
Каждая из следующих q строк содержит si, ti — непустые последовательности символов «+» и «-» одинаковой длины, разделённые одним пробелом. Эта строка означает, что в тесте номер i из исходной последовательности состояний ячеек si требуется получить итоговую последовательность ti.
Выходные данные должны содержать q строк, где i-я строка равна «Yes», если из исходной последовательности состояний ячеек si можно получить итоговую последовательность ti, или «No» в противном случае.
3 ++- +++ ++-- ++++ ++-+--+- ++++++++
Yes No Yes
3 ++-+-- ++---- ++-+-- +++--- -++- -++-
Yes No Yes
Победитель студенческой олимпиады получил предложения о стажировке от двух университетов. При подготовке планов обучения он узнал рейтинг качества преподавания каждой дисциплины в этих университетах.
Программа обучения первого университета состоит из последовательности перечисленных в хронологическом порядке n различных дисциплин a1, a2, ..., an, имеющих рейтинги x1, x2, ..., xn соответственно. Программа обучения второго университета состоит из последовательности перечисленных в хронологическом порядке m различных дисциплин b1, b2, ..., bm, имеющих рейтинги y1, y2, ..., ym соответственно.
Студент имеет возможность составить план обучения в первом университете таким образом, чтобы изучить дисциплины на позициях учебной программы с la по ra включительно (1 ≤ la ≤ ra ≤ n), либо отказаться от стажировки в первом университете. Аналогично он может составить план обучения во втором университете таким образом, чтобы изучить дисциплины на позициях учебной программы с lb по rb включительно (1 ≤ lb ≤ rb ≤ m), либо отказаться от стажировки во втором университете.
Изучать одну и ту же дисциплину дважды в разных университетах не имеет смысла, поэтому все дисциплины в двух выбранных планах обучения должны быть различны.
Требуется написать программу, которая определит планы обучения студента таким образом, чтобы получить наибольшую возможную сумму рейтингов изучаемых дисциплин.
Первая строка входных данных содержит целые числа n и m — количество дисциплин в программах обучения первого и второго университетов (1 ≤ n, m ≤ 500 000).
Вторая строка входных данных содержит n целых чисел ai — дисциплины, входящие в программу обучения первого университета, перечисленные в хронологическом порядке (1 ≤ ai ≤ n + m).
Третья строка входных данных содержит n целых чисел xi — рейтинги дисциплин, входящих в программу обучения первого университета, перечисленные том же порядке, что и дисциплины ai (1 ≤ xi ≤ 109).
Четвёртая строка входных данных содержит m целых чисел bi — дисциплины, входящие в программу обучения второго университета, перечисленные в хронологическом порядке (1 ≤ bi ≤ n + m).
Пятая строка входных данных содержит m целых чисел yi — рейтинги дисциплин, входящих в программу обучения второго университета, перечисленные том же порядке, что и дисциплины bi (1 ≤ yi ≤ 109).
Первая строка выходных данных должна содержать целое число r — наибольшую возможную сумму рейтингов дисциплин.
Вторая строка выходных данных должна содержать целые числа la, ra — позиции в учебной программе первой и последней дисциплин, входящих в план обучения в первом университете, либо «0 0», если студент отказался от стажировки в первом университете.
Третья строка выходных данных должна содержать целые числа lb, rb — позиции в учебной программе первой и последней дисциплин, входящих в план обучения во втором университете, либо «0 0», если студент отказался от стажировки во втором университете.
Если возможных правильных ответов несколько, разрешается вывести любой из них.
В первом тесте из условия приведённые планы обучения в университетах приводят к суммарному рейтингу дисциплин (7 + 4 + 10 + 1 + 5) + (5 + 3 + 4) = 27 + 12 = 39. Если бы студент выбрал только вторую и третью дисциплины в первом университете и весь курс обучения во втором университете, суммарный рейтинг дисциплин был бы (7 + 4) + (3 + 5 + 3 + 4 + 12) = 11 + 27 = 38.
Во втором тесте из условия первая и третья дисциплины во втором университете имеют настолько высокий рейтинг по сравнению с соответствующими дисциплинами первого университета, что наиболее выгодный вариант — пройти целиком стажировку во втором университете и отказаться от стажировки в первом университете.
7 5 3 1 4 8 6 9 2 2 7 4 10 1 5 3 9 2 11 3 8 3 5 3 4 12
39 2 6 2 4
2 3 1 2 1 4 2 3 1 17 2 15
34 0 0 1 3
3 3 4 2 1 10 1 2 5 4 2 1 2 9
19 1 1 3 3