Стек(35 задач)
Дек(6 задач)
Список(7 задач)
Префиксные суммы(минимумы, ...)(2 задач)
Рассмотрим последовательность, состоящую из круглых, квадратных и фигурных скобок. Последовательность называется правильной, если ее можно получить из какого-либо математического выражения вычеркиванием всех символов, кроме скобок. Формальное определение правильной скобочной последовательности таково:
1. Пустая последовательность является правильной.
2. Если A – правильная скобочная последовательность, то (A), [A] и {A} – правильные скобочные последовательности.
3. Если A и B – правильные скобочные последовательности, то AB – правильная скобочная последовательность.
По данной скобочной последовательности определите, является ли она правильной.
Программа получает на вход последовательность из скобок (открывающихся и закрывающихся скобок трех видов). Длина последовательности не превышает 255 символов. Последовательность не содержит пробелов (но после последнего символа могут идти пробелы и переходы на новую строку).
Проверьте, является ли эта последовательность правильной. Выведите слово yes, если последовательность правильная и слово no в противном случае.
()
yes
)
no
К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.
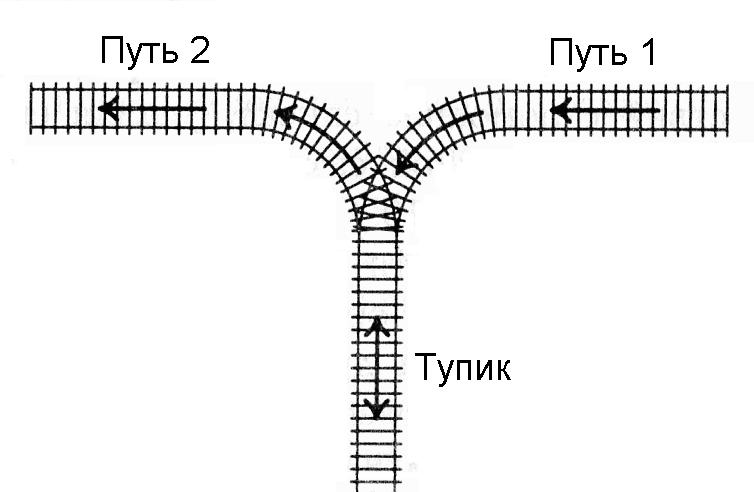
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).
Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.
Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:
Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.
Если выстроить вагоны по порядку невозможно, выведите одно число 0.
Примеры
| Входные данные | Выходные данные |
| 3 3 2 1 | 1 3 2 3 |
| 4 4 1 3 2 | 1 2 2 1 1 2 2 3 |
| 3 2 3 1 | 0 |
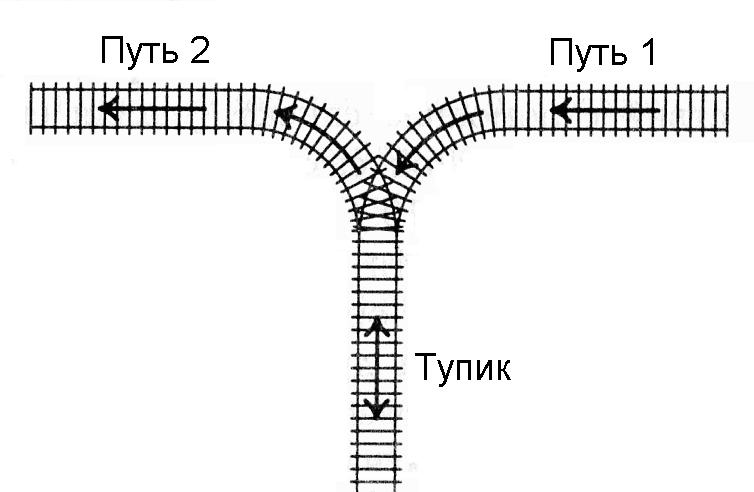
К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика). Напишите программу, определяющую, можно ли это сделать.
Вводится число N — количество вагонов в поезде (1≤N≤100). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.
Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите сообщение YES, если это сделать нельзя, выведите NO.
Примеры
| Входные данные | Выходные данные | Комментарии |
| 3 3 2 1 | YES | Надо весь поезд завезти в тупик, а затем целиком вывезти его на 2-й путь. |
| 4 4 1 3 2 | YES | Сначала надо в тупик завезти два вагона, один из которых оставит в тупике, а второй — вывезти на 2-й путь, после чего завезти в тупик еще два вагона и вывезти 3 вагона, стоящие в тупике, на 2-й путь |
| 3 2 3 1 | NO |
|
Дано N целых чисел. Требуется выбрать из них три таких числа, произведение которых максимально.
Дано N целых чисел. Требуется выбрать из них три таких числа, произведение которых максимально.
Во входном файле записано сначала число N — количество чисел в последовательности (3≤N≤106). Далее записана сама последовательность: N целых чисел, по модулю не превышающих 30000.
В выходной файл выведите три искомых числа в любом порядке. Если существует несколько различных троек чисел, дающих максимальное произведение, то выведите любую из них.
9 3 5 1 7 9 0 9 -3 10
9 10 9
3 -5 -30000 -12
-5 -30000 -12
Для транспортирования материалов из цеха А в цех В используется конвейер. Материалы упаковываются в одинаковые контейнеры и размещаются на ленте один за одним в порядке изготовления в цехе А. Каждый контейнер имеет степень срочности обработки в цехе В. Для упорядочивания контейнеров по степени срочности используют накопитель, который находится в конце конвейера перед входом в цех В. Накопитель работает пошагово, на каждом шаге возможны следующие действия:
накопитель перемещает первый контейнер из ленты в цех В;
накопитель перемещает первый контейнер из строки в склад (в складе каждый следующий контейнер помещается на предыдущий);
накопитель перемещает верхний контейнер из склада в цех В.
Напишите программу, которая по последовательности контейнеров определит, можно ли упорядочить их по степени срочности пользуясь описанным накопителем.
Входной файл в первой строке содержит количество тестов N. Далее следует N строк, каждый из которых описывает отдельный тест и содержит целое число K (1 ≤ K ≤ 10000) — количество контейнеров в последовательности и K действительных чисел — степеней срочности контейнеров в порядке их поступления из цеха А (меньшим числам соответствует большая степень срочности).
Каждая строка выходного файла должна содержать ответ для одного теста. Необходимо вывести 1, если необходимое упорядочивание возможно, или 0 в противном случае.
2 2 2.9 2.1 3 5.6 9.0 2.0
1 0