Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
У мальчика Васи есть \(N\) шоколадок (возможно, разного веса). Вася пригласил к себе в гости \(K\) своих друзей и хочет подарить им шоколадки. Чтобы никому из друзей не было обидно, Вася решил раздать шоколадки так, чтобы каждому другу досталось одно и то же количество шоколада (т.е. суммарный вес шоколадок, доставшихся каждому другу, должен быть одинаковым). Вася может раздать все свои шоколадки, может раздать лишь часть, но, поскольку он — очень гостеприимный мальчик, он не хочет оставлять друзей совсем без шоколада (т.е. сумма весов шоколадок, доставшихся каждому другу, должна быть строго положительной). Все шоколадки красиво упакованы, т.е. делить их на части нельзя.
Определите, сколько у Васи есть способов раздать шоколад своим друзьям. Два способа считайте различными тогда и только тогда, когда существует шоколадка, которая в одном способе досталась некоторому другу, а в другом — другому другу или вовсе не была отдана друзьям.
В первой строке входного файла находятся два натуральных числа \(N\) и \(K\) (\(1 \leq N \leq 15\), \(1 \leq K \leq 15\)) — количество шоколадок у Васи и количество друзей, которых Вася пригласил в гости. Во второй строке содержатся \(N\) натуральных чисел — веса шоколадок. Ни один из весов не превосходит \(1000\).
Выведите в выходной файл одно число — количество способов раздать шоколадки друзьям.
Во втором примере возможные распределения шоколадок следующие:
5 4 1 2 1 1 1
24
3 2 1 1 2
4
Готовясь к бою, хан Гирей пронумеровал всех воинов своего войска натуральными числами от 1 до N. Поскольку воины умеют сражаться, но не умеют считать, при любом построении в шеренгу они выстраиваются в произвольном порядке. Одного или несколько воинов, стоящих в шеренге, будем называть отрядом. Отряд назовем правильным, если номера этих воинов в том порядке, в котором они стоят в шеренге, образуют упорядоченную по возрастанию последовательность чисел. Среди всех правильных отрядов хан Гирей выбирает ударный отряд – самый большой по количеству воинов. Так, в шеренге 1 3 2 4 из четырех воинов ударными являются отряды 1 3 4 и 1 2 4, а отряд 1 4 – один из правильных, но не ударный. Некоторые воины являются личными телохранителями хана Гирея. Требуется составить программу, определяющую количество таких шеренг, в которых телохранители хана образуют ударный отряд.
В первой строке входного файла задано натуральное число N – общее количество воинов (1 ≤ N ≤ 15). Во второй строке задано натуральное число K – количество телохранителей хана (1 ≤ K ≤ N). В третьей строке через пробел указаны K различных натуральных чисел, не превосходящих N, – номера телохранителей хана в порядке возрастания.
Выходной файл должен содержать единственное число – количество различных расстановок всех воинов в шеренгу так, чтобы все телохранители хана были ударным отрядом в каждой из таких расстановок.
В первом примере войско состоит из пяти воинов. Ударный отряд должен состоять из трех воинов с номерами 1, 3 и 4. Этому условию удовлетворяют следующие 11 шеренг: (1, 3, 2, 5, 4), (1, 3, 5, 2, 4), (1, 3, 5, 4, 2), (1, 5, 3, 2, 4), (1, 5, 3, 4, 2), (2, 1, 3, 5, 4), (2, 1, 5, 3, 4), (2, 5, 1, 3, 4), (5, 1, 3, 2, 4), (5, 1, 3, 4, 2), (5, 2, 1, 3, 4).
Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы успешно пройдены.
5 3 1 3 4
11
3 3 1 2 3
1
1 1 1
1
Саша увлекается программированием компьютерных игр. Вот уже три для он пишет новую игру для сотового телефона под названием "Битва титанов". Героями игрушки являются оловянные солдатики. В качестве прототипа для описания действий оловянного солдатика Саша взял шахматную ладью.
Шахматная ладья - это фигура, которая может перемещаться на любое количество клеток по вертикали или горизонтали. Ладьи не могут перемещаться за препятствия. Задача - вычислить максимальное количество ладей, которые можно поставить на доске так, чтобы никакие две не били друг друга. Это означает, что конфигурация правильна при условии, что никакие две ладьи не находятся на одной горизонтали или вертикали в пределах видимости друг друга.
Следующий пример показывает пять изображений. Первое изображение является пустым, второе и третье изображения показывают правильные конфигурации, а четвертый и пятый рисунок - примеры неправильных конфигураций.
Помогите Саше поскорее закончить программу и вычислите максимальное количество ладей на заданной конфигурации доски.
Во входном файле в первой строке содержится натуральное число \(N\) - размер доски, не превышающий 4. Следующие \(N\) строк содержат по \(N\) символов — описание шахматной доски, причем символ '.' указывает пустую клетку, а символ верхнего регистра 'X' указывает препятствие. Во входном файле нет пробелов.
Выведите максимальное количество ладей на правильной конфигурации доски.
4 .X.. .... XX.. ....
5
Командная олимпиада, о которой идёт речь в этой задаче, проходила по тем же правилам, что и олимпиада, в которой вы сейчас участвуете. Возможно, за одним исключением: на ней было введено ограничение на суммарное число посылок от одной команды, которые можно было потратить как на одну задачу, так и распределить их по всем задачам некоторым образом.
Как и сегодня, за час до окончания олимпиады таблица результатов была «заморожена». Каково же было удивление участников, когда при подведении итогов выяснилось, что в окончательной таблице все команды расположились строго в обратном порядке (по отношению к порядку, зафиксированному «заморозкой»). Так как в окончательной таблице результатов посылки участников не отражены, вам предлагается определить, могло ли такое быть в принципе, или это результат технического сбоя системы.
Первая строка содержит три натуральных числа: N — количество команд, K — количество задач, L — лимит на суммарное число посылок по задачам (N ≤ 1000, K ≤ 12, K ≤ L ≤ 200).
Далее следуют N строк, описывающих саму таблицу на момент заморозки. i-я строка содержит название команды (строка из латинских символов и цифр длины не более 50) и K элементов, показывающих успех команды по каждой из задач. j-й элемент таблицы имеет вид * Wrong(Time), где:
* — знак ‘ + ’ или ‘ - ’, показывающий, решила ли команда задачу;
Wrong — количество неуспешных посылок по данной задаче;
Time — минута, на которой команда сдала задачу (0 ≤ Time ≤ 239); если данная задача ещё не была решена, Time = 0.
Команды упорядочены от первого места на момент заморозки к последнему. Напоминаем, что команды сортируются по числу решённых задач, а при равном количестве — по увеличению штрафного времени, которое складывается из времени сдачи задачи и общего количества неудачных попыток по решённым задачам, умноженного на 20. Продолжительность олимпиады — 5 часов.
Гарантируется, что ни одна команда не превысила лимит на число посылок и что никакие две команды не имеют одинаковый с точки зрения сортировки результат.
Если порядок команд теоретически мог измениться за последний час соревнований на обратный, то сначала выведите строку «Possible», а затем подробную таблицу окончательных результатов в формате, аналогичном таблице из входного файла (см. пример). Если соревнование так закончиться не могло, то выведите единственную строку «Impossible».
3 3 10
winner +2(235) +3(170) -2(0)
middle -2(0) +1(30) -0(0)
looser -1(0) +5(30) -0(0)
Possible
looser +1(240) +5(30) +0(240)
middle +5(241) +1(30) +0(240)
winner +2(235) +3(170) +2(240)
2 2 20
winner +10(1) +0(10)
looser -0(0) +1(1)
Impossible
Маленький Вася очень любит поезда. На день рождения ему подарили игрушечную железную дорогу. В комплект к железной дороге входит поезд, состоящий из \(n\) вагонов, пронумерованных числами от 1 до \(n\).
Любимым занятием Васи стала сортировка поездов с использованием специального сортировочного тупика.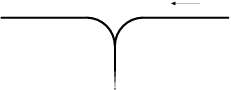
Справа к тупику подъезжает поезд, составленный из всех \(n\) вагонов. Затем вагоны по одному загоняются в сортировочный тупик и выгоняются из него налево. Васе нравится, если ему удается отсортировать поезд с помощью сортировочного тупика — добиться того, чтобы слева от тупика вагоны были расположены по порядку от 1 до \(n\).
Например, пусть в исходном поезде 4 вагона, которые следуют в порядке 3, 1, 2, 4. Его можно отсортировать следующим образом. Загоняем вагон 3 в тупик. Загоняем вагон 1 в тупик. Выгоняем вагон 1 из тупика. Загоняем вагон 2 в тупик. Выгоняем вагон 2 из тупика. Выгоняем вагон 3 из тупика. Загоняем вагон 4 в тупик. Выгоняем вагон 4 из тупика.
Не все поезда можно отсортировать таким образом. Например, поезд из 3 вагонов, следующих в порядке 2, 3, 1, отсортировать нельзя.
Вася выписал на листке в лексикографическом порядке все поезда длины \(n\), которые можно отсортировать с помощью тупика. Поезд \((a_1, a_2, \ldots, a_n)\) идет раньше поезда \((b_1, b_2, \ldots, b_n)\) в лексикографическом порядке, если существует такое \(i\) (\(1 \le i \le n\)), что для всех \(j < i\) выполняется \(a_j = b_j\), а \(a_i < b_i\). Например, все поезда из трех вагонов, которые можно отсортировать с помощью тупика, в лексикографическом порядке выписываются следующим образом: \((1, 2, 3)\), \((1, 3, 2)\), \((2, 1, 3)\), \((3, 1, 2\)), \((3, 2, 1)\).
Вася потерял свой листок, и его интересует вопрос: какой поезд был выписан на его листке под номером \(k\). Помогите ему выяснить это.
Входной файл содержит два целых числа — \(n\) и \(k\) (\(1 \le n \le 30\), \(1 \le k \le 10^{18}\)).
Выведите в выходной файл \(n\) целых чисел: \(k\)-й в лексикографическом порядке поезд из \(n\) вагонов, который можно отсортировать с помощью тупика.
Если с помощью тупика можно отсортировать менее \(k\) поездов из \(n\) вагонов, выведите \(-1\).
4 1
1 2 3 4
4 3
1 3 2 4
4 15
-1