Палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево. Подпалиндромом данной строки называется последовательность символов из данной строки (в том же порядке, но не обязательно идущих подряд), являющаяся палиндромом. Например, HELOLEH является подпалиндромом строки HTEOLFEOLEH. Напишите программу, находящую в данной строке подпалиндром максимальной длины.

На листке записано в одну строку \(N\) (\(2 \leq N \leq 100\)) целых положительных чисел. Каждое число не превышает 200. Играют двое. За каждый ход можно зачеркивать крайнее число либо слева, либо справа. Зачеркнутое число добавляется к очкам игрока. \(N\) – четное. Игру начинает первый игрок. Необходимо вывести максимально возможную сумму очков для первого игрока при условии, что противник играет наилучшим образом..

Антон - большой любитель компьютерных игр. Совсем недавно вышла новая игра Heroes of Keyboard and Mouse, и он, конечно же, сразу ее купил и установил на свой компьютер. Эта игра относится к жанру квестов, и поэтому ее прохождение сводится к последовательному выполнению ряда заданий (квестов).

Один из квестов, над которым Антон бьется уже не первый день состоит в том, что требуется открыть замок. Замок состоит из \(n\) шестеренок, стоящих в ряд - \(i\)-ая из шестеренок имеет \(s_i\) зубцов, на каждом из которых написано число от \(0\) до \(s_i - 1\). Первая шестеренка зацеплена только со второй, вторая зацеплена с первой и третьей, третья - со второй и четвертой, ..., \((n-1)\)-ая - с \((n-2)\)-ой и \(n\)-ой, \(n\)-ая только с \((n-1)\)-ой.

На замке имеется \(n\) окошечек и \(n\) ручек - в \(i\)-ое окошко можно видеть число, написанное на одном из зубцов \(i\)-ой шестеренки, а с помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. При этом числа на шестеренках расположены таким образом, что если до поворота \(i\)-ой из них по часовой стрелке на одно деление в \(i\)-ом окошке было видно число \(x\), то после поворота будет видно число \((x+1) \bmod s_i\). Аналогично, после поворота против часовой стрелки на одно деление вместо числа \(x\) будет видно число \((x-1+s_i) \bmod s_i\). Разумеется, если шестеренку повернуть по часовой стрелке, то непосредственно зацепленные с ней шестеренки повернутся против часовой стрелки, и наоборот, если шестеренку повернуть против часовой стрелки, то они повернутся по часовой стрелке. Слева на рис.1 показано положение шестеренок до поворота первой из них по часовой стрелке, справа на рис. 1 показано положение шестеренок после указанного поворота. Более толстыми линиями нарисован тот зубец шестеренки, число на котором видно в соответствующее окошко замка.

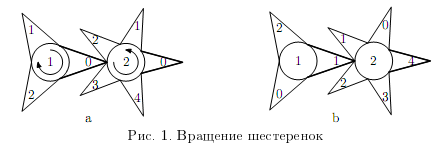
Изначально замок находится в состоянии, в котором в \(i\)-ое окошко видно число \(a_i\). Для того, чтобы его открыть, необходимо перевести его в состояние, в котором в \(i\)-ое окошко видно число \(b_i\).

С помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. Разумеется, если повернуть \(i\)-ую шестеренку, то придут в движение и все шестеренки, с которыми она соединена - напрямую или через другие шестеренки. Поворот любой шестеренки на одно деление занимает одну секунду. Кроме этого, если \(i\)-ая шестеренка находится в таком состоянии, что в \(i\)-ое окошко видно число \(b_i\) (то есть, она находится в положении, соответствующем требуемому состоянию замка), то ее можно вдавить, нажав на ее ручку. В результате этого \(i\)-ая шестеренка перестает быть соединенной с \((i-1)\)-ой и \((i+1)\)-ой (если, конечно, они существуют). Вдавленная шестеренка остается в таком состоянии навсегда. На то, чтобы нажать на ручку и вдавить шестеренку требуется \(k\) секунд. На рис. 2 слева показано положение шестеренок до вдавливания второй из них, а справа - после вдавливания и после поворота первой по часовой стрелке, а третьей - против. Отметим, что после вдавливания второй шестеренки первая и третья вращаются независимо друг от друга.

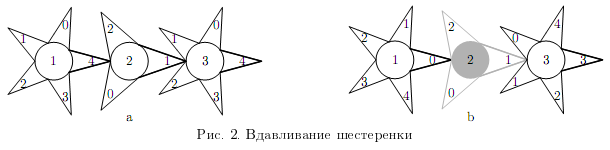
Для того, чтобы выполнить квест, Антону необходимо открыть замок как можно быстрее. Напишите программу, которая по описанию замка, его начального состояния и требуемого состояния, вычислит минимальное время, за которое Антон может открыть замок.