Темы --> Информатика --> Язык программирования
    Процедуры и функции(96 задач)
    Массивы(232 задач)
    Типы данных(356 задач)
    Циклы(177 задач)
    Условный оператор (if)(164 задач)
    Python(260 задач)
    Standard Template Library(2 задач)
---> 52 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 2 3 4 5 6 7 8 >> Отображать по:
#1929
Новое слово в рекламе
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
64 megabytes

В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.

Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.

К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому было решено использовать их вторично.

Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.

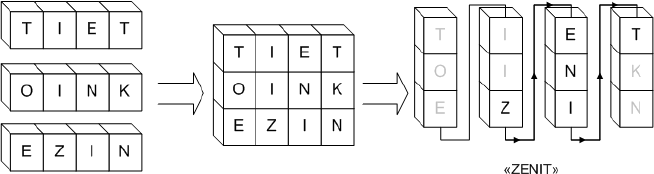
Таким образом, можно получить рекламную надпись для нового клиента. При этом из эстетических соображений при прочтении конечной надписи разрывы в виде закрашенных букв недопустимы.

После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка «TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».

Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.

Входные данные

Первая строка входного файла содержит два натуральных числа \(N\) и \(L\) — число различных типов блоков на складе и длина каждого блока соответственно (\(1\le N\le100\), \(1\le L\le100\)). Последующие \(N\) строк содержат по одной записи длиной \(L\), состоящей из строчных латинских букв — надписи на блоках соответствующего типа. Надписи на блоках разных типов не совпадают.

Последняя строка входного файла содержит новую рекламную надпись \(s\) — строку, состоящую только из строчных латинских букв (\(1\le|s|\le200\)). Можно считать, что на складе находится неограниченное число блоков каждого типа.

Выходные данные

В первой строке выходного файла необходимо вывести натуральное число \(K\) — минимальное количество блоков, которое нужно использовать для составления новой рекламы. Следующая строка должна содержать \(K\) чисел — номера типов блоков, которые нужно для этого использовать, перечисляя их сверху вниз. Типы блоков нумеруются с единицы в порядке их задания во входном файле.

Если ответов несколько, выведите любой из них. Если решения не существует, выведите в выходной файл число \(-1\).

Примеры
Входные данные
3 4
tiet
oink
ezin
zenit
Выходные данные
3
1 2 3
Входные данные
2 11
sillysample
happysample
sam
Выходные данные
1
2
Входные данные
2 3
baa
aab
bb
Выходные данные
2
2 2
Входные данные
2 3
aaa
bbb
cc
Выходные данные
-1
#2972
Спички
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Вдоль прямой выложены три спички. Необходимо переложить одну из них так, чтобы при поджигании любой спички сгорали все три. Для того чтобы огонь переходил с одной спички на другую, необходимо чтобы эти спички соприкасались (хотя бы концами).

Требуется написать программу, определяющую, какую из трех спичек необходимо переместить.

Входные данные

Вводятся шесть целых чисел через пробел: l1, r1, l2, r2, l3, r3 –– координаты первой, второй и третьей спичек соответственно (0 ≤ li < ri ≤ 100). Каждая спичка описывается координатами левого и правого концов по горизонтальной оси OX.

Выходные данные

Выведите номер искомой спички. Если возможных ответов несколько, то выведите наименьший из них. В случае, когда нет необходимости перемещать какую-либо спичку, выведите 0. Если же требуемого результата достигнуть невозможно, то выведите -1.

Примечание

Оценка: 25 баллов

Примеры
Входные данные
0 2 4 5 3 6
Выходные данные
1
Входные данные
1 2 9 10 12 20
Выходные данные
3
Входные данные
1 5 0 1 4 8
Выходные данные
0
#3014
Поклейка обоев
  
Темы: [Целые числа]

Пете нужно оклеить обоями стену размером N метров в высоту и M метров в ширину. Для поклейки используются обои, которые продаются рулонами. Каждый рулон имеет ширину 1 метр и длину K метров. Обои клеятся на стену вертикальными полосами (сверху вниз). При этом Петя хочет так поклеить обои, чтобы горизонтальных стыков разных кусков не было (то есть один цельный кусок клеится от потолка до пола). От рулона можно отрезать куски нужного размера (иногда при этом может оставаться кусок, меньшего размера, который поэтому не может быть поклеен, этот кусок идет в отходы).

По данным числам N, M и K определите наименьшее количество рулонов, которое нужно купить Пете, чтобы оклеить всю стену.

Входные данные

Вводятся натуральные числа N, M и K (1 ≤ N ≤ 100, 1 ≤ M ≤ 100, N ≤K ≤100).

Выходные данные

Выведите одно число - количество рулонов, которые должен купить Петя.

Примеры
Входные данные
10
5
25
Выходные данные
3
Входные данные
3
6
9
Выходные данные
2
#3016
Списывание
  
Темы: [Цикл for]

На контрольной работе N учеников сидят в ряд. Для каждого ученика известно, какую оценку он получил бы, если бы писал эту контрольную самостоятельно (оценка — это число от 2 до 5). Однако ученики могут писать контрольную не только самостоятельно, но и списывать у своего соседа, но только если сосед пишет контрольную самостоятельно. В этом случае списывающий получит такую же оценку, какую получит тот, у кого он списал.

А именно (правила применяются строго в указанном порядке):

  • Школьники, которые знают материал на 5, будут писать контрольную самостоятельно.
  • Школьник, который знает материал на 4, если он сидит рядом с тем, кто знает на 5, будет списывать у него, а в противном случае будет писать самостоятельно.
  • Школьник, который знает на 3, если он сидит рядом с тем, кто знает на 5, будет списывать у него. Если среди его соседей знающего на 5 нет, но есть тот, кто знает на 4, и при этом пишет самостоятельно, то троечник будет списывать у него. В противном случае будет писать самостоятельно.
  • Аналогично школьник, знающий на 2 — из соседей, которые пишут самостоятельно, выберет того, кто знает лучше, и спишет у него. А если таких нет (или оба его соседа также знают на 2), то будет писать самостоятельно.

Определите, кто какую оценку в итоге получит.

Входные данные

Вводится число N (1<=N<=10) - количество учеников, и далее последовательность из N чисел, описывающая, кто на какую оценку может написать контрольную, если будет писать самостоятельно.

Выходные данные

Выведите N чисел - оценки, которые получат ученики за контрольную.

Примечания к примерам тестов

1. Первый и пятый ученики будут писать самостоятельно. Второй спишет у первого, а четвертый — у пятого (в итоге также получат пятерки). Третьему не у кого списывать, так как его соседи будут писать работу не самостоятельно.

2. Второй и четвертый спишут у третьего, пятый — у шестого.

Примеры
Входные данные
5
5
2
3
4
5
Выходные данные
5
5
3
5
5
Входные данные
6
2
2
3
2
2
4
Выходные данные
2
3
3
3
4
4
#3017
Последовательности
  
Темы: [Цикл while]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Рассмотрим последовательности чисел. Первая последовательность состоит из одного числа K. Каждая следующая последовательность чисел описывает предыдущую по такому правилу.

Просматриваем описываемую последовательность слева направо и разбиваем на отрезки, состоящие из подряд идущих равных чисел (причем все идущие подряд одинаковые числа всегда объединяем в один отрезок). Далее каждый такой отрезок описываем двумя числами — первое число говорит, сколько раз повторяется одно и то же число, второе число говорит, какое именно число повторяется. Записываем эти пары последовательно в соответствии с отрезками слева направо, и получаем новую последовательность (см. примеры ниже).

Например, для K=2 последовательности получатся такими:

№ Последовательность Как ее читать (слова в описании соответствуют числам текущей последовательности слева направо, и описывают предыдущую последовательность)
1 2 Исходная последовательность
2 1 2 Одна «двойка»
3 1 1 1 2 Одна «единица», одна «двойка»
4 3 1 1 2 Три «единицы», одна «двойка»
5 1 3 2 1 1 2 Одна «тройка», две «единицы», одна «двойка»
6 1 1 1 3 1 2 2 1 1 2 Одна «единица», одна «тройка», одна «двойка», две «единицы», одна «двойка»

Напишите программу, которая по исходному числу K напечатает N-ую получающуюся последовательность.

Входные данные

Вводится число K (1 ≤ K ≤ 9) и число N (1 ≤ N ≤ 15).

Выходные данные

Ваша программа должна печатать N-ую последовательность, полученную из начальной последовательности, состоящей из одного числа K. Числа при выводе следует разделять пробелами.

Примеры
Входные данные
2
6
Выходные данные
1 1 1 3 1 2 2 1 1 2
Входные данные
2
1
Выходные данные
2
Входные данные
1
3
Выходные данные
2 1
Страница: << 2 3 4 5 6 7 8 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест