Темы --> Информатика --> Язык программирования
    Процедуры и функции(96 задач)
    Массивы(232 задач)
    Типы данных(356 задач)
    Циклы(177 задач)
    Условный оператор (if)(164 задач)
    Python(260 задач)
    Standard Template Library(2 задач)
---> 52 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 3 4 5 6 7 8 9 >> Отображать по:
#3018
Сравнения
  

Про три числа (обозначенных a, b, c) известны все результаты сравнения их друг с другом. Требуется расположить эти числа в порядке возрастания.

Входные данные

Вводятся три строки. В первой записан результат сравнения между собой чисел a и b в следующем формате. Первый символ — всегда a, третий символ — b (соответствующие маленькие латинские буквы), а между ними записан один из символов >, < или =. Во второй строке в таком же формате записан результат сравнения a и с (первый символ всегда a, третий — c), а в третьей строке — результат сравнения b и c (первый символ всегда b, третий — c). Гарантируется, что входные данные не противоречивы.

Выходные данные

Выведите символы a, b, c в порядке величины соответствующих им чисел — каждое следующее число должно быть больше либо равно предыдущему. Если два числа равны между собой, соответствующие переменные могут быть выведены в любом порядке. Символы должны быть выведены в одной строке без пробелов и других разделителей.

Примечание

Во втором примере ответ cba также является верным. Обратите внимание, если вариантов ответа несколько — не нужно выводить их все, ваша программа должна вывести ровно один вариант ответа.

Примеры
Входные данные
a>b
a>c
b>c
Выходные данные
cba
Входные данные
a=b
a>c
b>c
Выходные данные
cab
cba
#3139
Лицензионные ключи
  
Темы: [Строки]

Компания Macrohard выпустила в свет новую версию операционной системы «Frames» («Рамки») и теперь стремится внедрить ее на рынок информационных технологий. Каждая фирма, заказывающая новую версию «Рамок», получает лицензионные ключи от компании Macrohard по следующим правилам:

  • каждой копии присваивается уникальный 25-разрядный ключ, состоящий из цифр и заглавных букв латинского алфавита. Код разбивается на группы по 5 символов, которые разделяются между собой знаком «-»
  • по каждому ключу можно вычислить его контрольную сумму по следующему правилу: необходимо сложить веса значащих символов и взять остаток от деления этой суммы на некое число P, где вес символа есть
    • значение цифры, если символ является цифрой (то есть вес цифры 5 равен пяти)
    • порядковый номер буквы в латинском алфавите плюс 9 (то есть вес буквы F равен 15)
Например, для кода 12345-12345-12345-12345-12345 при P = 11 контрольная сумма равна (1+2+3+4+5)*5 mod 11 = 9
  • контрольная сумма является идентификатором фирмы, которая покупает операционные системы, следовательно, оно должно быть различным для разных юридических лиц.

Операционной системой заинтересовался один влиятельный человек, пожелавший установить ее на свой персональный компьютер. Вам, как работнику отдела лицензирования Macrohard, поручено сгенерировать новый ключ, который не только не повторяется с выданными ранее ключами, но и обладает новой (не используемой ранее) контрольной суммой. Требуется написать программу, которая решает эту задачу.

Входные данные

В первой строке входного файла содержится два натуральных числа N и P (1 ≤ N ≤ 30000, 1 ≤ P ≤ 1000), где N – число уже использованных ключей, P – число, используемое для подсчета контрольной суммы. В следующих N строках следуют ключи, которые задаются в виде
XXXXX-XXXXX-XXXXX-XXXXX-XXXXX, где X – значащий символ (цифра или буква латинского алфавита).

Выходные данные

В выходной файл требуется вывести новый уникальный ключ в соответствии с указанным форматом, обладающий уникальной контрольной суммой. В случае, если такой ключ сгенерировать невозможно, выведите слово «Impossible».

Ввод
Вывод
3 5
23545-14978-59345-87926-52496     
67955-58818-19438-55659-02068    
99185-57241-15114-39158-36125
01389-28172-62843-79648-28129
5 3
BGPOV-D618J-FTN7L-4QWZJ-E6P8S     
7K3J3-I8076-58COS-0066F-9UAT4     
7S17C-YI099-1UC85-5S9PB-772LT     
TN2I4-TC1Z6-1OLI6-LT43G-9JMD3     
73OQ3-A9NBJ-N7UT7-AI349-XYJDT
1APMP-RSO53-G743I-F5TK6-R6487
5 4
7911L-5D41U-0N09C-34T16-5D0KI     
FRLAX-RE1Y1-WFVU0-88R56-C5D4V     
RUG51-IR00T-8L812-R6056-7OM59     
804F2-L7292-I12PX-14NDO-02LEW     
J3QQ4-H7H2V-2HCH4-M3HK8-6M8VW
Impossible
#3181
Ролевая игра
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Вася готовит инвентарь для ролевой игры. В игре должны принять участие \(n\) игроков, каждый из которых будет изображать персонажа фантастического мира. В процессе игры каждый персонаж будет обладать некоторым уровнем \(x\), который представляет собой целое число от \(1\) до \(m\).

Для обозначения уровня планируется использовать специальные значки двух цветов. Белый значок обозначает один уровень, а красный значок — k уровней. Игрок, изображающий персонажа с уровнем \(x\), должен иметь \(a\) белых значков и \(b\) красных значков, чтобы сумма \((a + bk)\) была равна \(x\). При этом персонажу не разрешается иметь более чем \((k - 1)\) белых значков.

Значки для игры готовятся заранее, однако уровни персонажей заранее неизвестны. Для успешного проведения игры всем персонажам необходимо выдать соответствующее их уровням количество значков. Возникает вопрос: какое минимальное суммарное количество значков необходимо подготовить для успешного проведения игры при любых уровнях участвующих персонажей.

Требуется написать программу, которая по заданным числам \(n\), \(m\) и \(k\) вычисляет минимальное количество значков, которое необходимо подготовить для успешного проведения игры.

Входные данные

Входной файл содержит расположенные в одной строке три целых числа: \(n\), \(m\) и \(k\) (\(1 \le n \le 10^4\), \(1 \le m \le 10^5\), \(1 \le k \le 10^5\)).

Выходные данные

В выходном файле должно содержаться одно целое число — минимальное количество значков, которое требуется подготовить.

Примечание

В приведенном примере необходимо подготовить 6 красных и 3 белых значка.

Примеры
Входные данные
3 4 2
Выходные данные
9
#3206
Шахматная доска
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

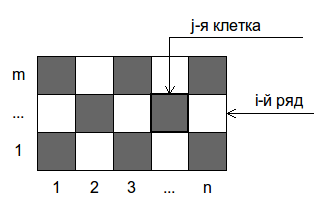Аня разделила доску размера \(m \times n\) на клетки размера \(1 \times 1\) и раскрасила их в черный и белый цвет в шахматном порядке. Васю заинтересовал вопрос: клеток какого цвета получилось больше — черного или белого.

Для того, чтобы выяснить это, он спросил у Ани, в какой цвет она раскрасила \(j\)-ю клетку в \(i\)-м ряду доски. По этой информации Вася попытался определить, клеток какого цвета на доске больше.

Требуется написать программу, которая по размерам доски и цвету \(j\)-й клетки в \(i\)-м ряду определит, клеток какого цвета на доске больше — черного или белого.

Входные данные

Входной файл содержит пять целых чисел: \(m\), \(n\), \(i\), \(j\) и \(c\) (\(1 \le m, n \le 10^9\), \(1 \le i \le m\), \(1 \le j \le n\), \(с = 0\) или \(с = 1\)). Значение \(c = 0\) означает, что \(j\)-я клетка в \(i\)-м ряду доски раскрашена в черный цвет, а значение \(c = 1\) — в белый цвет.

Выходные данные

Выходной файл должен содержать одно из трех слов:

  • black, если черных клеток на доске больше,
  • white, если белых клеток на доске больше,
  • equal, если черных и белых клеток на доске поровну.

Примечание

Правильные решения для тестов, в которых \(1 \le m, n \le 100\), оцениваются из 50 баллов.

Примеры
Входные данные
3 5 1 1 0
Выходные данные
black
Входные данные
3 5 2 1 0
Выходные данные
white
Входные данные
4 4 1 1 1
Выходные данные
equal
#3207
Чемпионат по стрельбе
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Победитель школьного этапа олимпиады по информатике нашел дома в старых бумагах результаты чемпионата страны по стрельбе из лука, в котором участвовал его папа. К сожалению, листок с результатами сильно пострадал от времени, и разобрать фамилии участников было невозможно. Остались только набранные каждым участником очки, причем расположились они в том порядке, в котором участники чемпионата выполняли стрельбу.

Расспросив папу, школьник выяснил, что количество очков, которое набрал папа, заканчивается на 5, один из победителей чемпионата стрелял раньше, а папин друг, который стрелял сразу после папы, набрал меньше очков. Теперь он заинтересовался, какое самое высокое место мог занять его папа на том чемпионате.

Будем считать, что участник соревнования занял \(k\)-е место, если ровно \((k - 1)\) участников чемпионата набрали строго больше очков, чем он. При этом победителями считались все участники чемпионата, занявшие первое место.

Требуется написать программу, которая по заданным результатам чемпионата определяет, какое самое высокое место на чемпионате мог занять папа победителя школьного этапа олимпиады по информатике.

Входные данные

Первая строка входного файла содержит целое число \(n\) — количество участников чемпионата страны по стрельбе (\(3 \le n \le 10^5\)).

Вторая строка входного файла содержит \(n\) положительных целых чисел, каждое из которых не превышает 1000, — очки участников чемпионата, приведенные в том порядке, в котором они выполняли стрельбу.

Выходные данные

В выходном файле должно содержаться одно целое число — самое высокое место, которое мог занять папа школьника. Если не существует ни одного участника чемпионата, который удовлетворяет, описанным выше условиям, выведите в выходной файл число 0.

Примечание

Правильные решения для тестов, в которых \(1 \le n \le 1000\), оцениваются из 50 баллов.

Примеры
Входные данные
7
10 20 15 10 30 5 1
Выходные данные
6
Входные данные
3
15 15 10
Выходные данные
1
Страница: << 3 4 5 6 7 8 9 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест