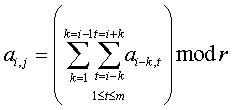Страница: << 35 36 37 38 39 40 41 >> Отображать по:
#1106
SMS
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

SMS-сообщения на мобильном телефоне марки MOBILO набираются только заглавными английскими буквами. Для набора буквы нужно нажать кнопку, на которой эта буква написана, при этом если эта буква написана первой, то кнопку нужно нажать один раз, если второй – то два раза и т.д. Устройство клавиатуры телефона приведено на рисунке.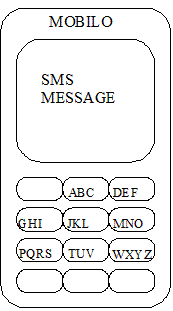

Таким образом, чтобы набрать слово SMS, нужно нажать следующие кнопки:

<PQRS> <PQRS> <PQRS> <PQRS> <MNO> <PQRS> <PQRS> <PQRS> <PQRS>

Для набора двух букв, которые находятся на одной кнопке, при наборе нужно сделать паузу между их вводом. Например, чтобы набрать BA, нужно два раза нажать кнопку <ABC>, затем сделать паузу и затем нажать кнопку <ABC> еще раз.

Если на кнопке написано три буквы, то как только эта кнопка нажата три раза подряд, последняя из написанных на ней букв сразу же добавляется в сообщение, а дальнейшие нажатия на эту кнопку воспринимаются как ввод следующей буквы. То же самое, если на кнопке написано 4 буквы. Таким образом, 4-х кратное нажатие на кнопку <ABC>, затем пауза, и затем нажатие на эту кнопку еще раз приведет к вводу текста CAA.

К сожалению, в силу произошедшего глюка, телефон стал иногда игнорировать паузы при вводе, а, иногда, наоборот, вести себя так, как будто была пауза тогда, когда паузы не было. Например, при вводе слова MOSCOW могло в итоге (как один из вариантов) получиться слово OMSCMNW.

Вы получили SMS-сообщение, набранное на этом телефоне. Известно, что изначально оно состояло из N символов. Напишите программу, которая определит количество вариантов исходных сообщений, которые при вводе могли превратиться в то, что вы получили (если вариантов окажется 0, то это будет означать, что у телефона сломалось что-то еще).

Входные данные

Сначала записана длина исходного сообщения N (1≤N≤80). Вторая строка содержит полученное SMS-сообщение – последовательность не более чем из 80 заглавных латинских букв.

Выходные данные

Выведите одно число – количество вариантов исходного сообщения.

Примеры
Входные данные
4
MAMA
Выходные данные
1
Входные данные
2
WWW
Выходные данные
2
Входные данные
10
MAMA
Выходные данные
0
#1107
Лягушачьи игры
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Имя входного файла: frogs.in
Имя выходного файла: frogs.out

В тридесятом царстве в новогодние праздники все лягушки собираются на самом большом болоте, чтобы поиграть в замечательную игру. Всего в этом царстве живет N зеленых лягушек и M коричневых. Для игры они выбирают на болоте N + M + 1 кочку, на первые N кочек слева садятся зеленые лягушки, а на последние M — коричневые (т. е. между ними находится одна кочка, на которой никто не сидит). Зеленые лягушки садятся лицом к коричневым лягушкам, а коричневые — к зеленым. Кочки настолько маленькие, что развернуться на них, не свалившись в болото, совершенно не возможно. Поэтому лягушки могут двигаться только вперед и не могут разворачиваться.

На каждом ходе игры одна из лягушек перепрыгивает с той кочки, где она сидит, на свободную кочку. При этом лягушка может прыгнуть на соседнюю кочку вперед, либо перепрыгнуть через одну кочку, если соседняя занята.

Чтобы праздник удался, зеленые лягушки должны оказаться на последних кочках, а коричневые — на первых. Порядок, в котором лягушки окажутся на кочках, не важен. Так как на праздник каждый раз приходит разное количество лягушек, то им каждый год приходится придумывать очередность прыжков. Напишите программу, которая поможет лягушкам составить план прыжков.

Поиграть в эту игру для случая N=M=3 можно по ссылке:

http://olympiads.ru/zaoch/2007/problems/frogs.swf

Входные данные

Во входном файле записаны два числа N и M (1≤N≤1000, 1≤M≤1000) – количество зеленых и коричневых лягушек соответственно.

Выходные данные

Выведите последовательность прыжков лягушек для достижения поставленной цели. Каждый прыжок можно задать одним числом — номером прыгающей лягушки (поскольку свободная кочка всегда ровно одна). Пронумеруем всех лягушек в соответствии с их начальным положением. Зеленые лягушки будут пронумерованы числами от 1 до N, а коричневые — с N+1 до N+M в порядке слева направо.

В первую строку выходного файла выведите число K — количество прыжков. K не должно превышать 107. Далее выведите K чисел — номера лягушек.

Если же достичь требуемой рассадки лягушек нельзя, выведите одно число –1.

Примеры
Входные данные
2 1
Выходные данные
5
2 3 2 1 3
#1150
Таблица
  

Рассмотрим прямоугольную таблицу размером n m. Занумеруем строки таблицы числами от 1 до n, а столбцы – числами от 1 до m. Будем такую таблицу последовательно заполнять числами следующим образом.

Обозначим через aij число, стоящее на пересечении i-ой строки и j-ого столбца. Первая строка таблицы заполняется заданными числами – a11, a12, …, a1m. Затем заполняются строки с номерами от 2 до n. Число aij вычисляется как сумма всех чисел таблицы, находящихся в «треугольнике» над элементом aij. Все вычисления при этом выполняются по модулю r.






























 

 

ai,j

















Более точно, значение aij вычисляется по следующей формуле:

 

Например, если таблица состоит из трех строк и четырех столбцов, и первая строка состоит из чисел 2,3,4,5, а r = 40 то для этих исходных данных таблица будет выглядеть следующим образом (взятие по модулю показано только там, где оно приводит к изменению числа):

2

3

4

5

5 = 2 + 3

9 = 2 + 3 + 4

12 = 3 + 4 + 5

9 = 4 + 5

23 = 2 + 3 + 4 + 5 + 9

0 = (2 + 3 + 4 + 5 + 5 + 9 + 12) mod 40 = 40 mod 40

4 = (2 + 3 + 4 + 5 + 9 + 12 + 9) mod 40 = 44 mod 40

33 = 3 + 4 + 5 + 12 + 9

Требуется написать программу, которая по заданной первой строке таблицы (a11, a12, …, a1m), вычисляет последнюю строку, как описано выше.

Входные данные

Первая строка входного файла содержит числа n, m и r (2 ≤ n, m ≤ 2000, 2 ≤ r ≤ 109) – число строк и столбцов таблицы соответственно, а так же число, по модулю которого надо посчитать ответ. Следующая строка содержит m целых чисел – первую строку таблицы: a11, a12, …, a1m. Все a1i неотрицательны и не превосходят 109.

Выходные данные

В первой строке выходного файла необходимо вывести m чисел – последнюю строку таблицы: an1, an2, …, anm.

Примеры
Входные данные
2 3 10
1 2 3
Выходные данные
3 6 5
Входные данные
3 3 10
1 1 1
Выходные данные
8 0 8
Входные данные
3 4 40
2 3 4 5
Выходные данные
23 0 4 33
#1151
Гомотетия
  

Гомотетией с центром O и коэффициентом k 0 называют преобразование плоскости, при котором точка O переходит сама в себя, а любая точка X O – в такую точку Y, что:

  • Y лежит на прямой OX;
  • OY = |k|OX;
  • при k >0 Y лежит на луче OX, при k <0 Y лежит на продолжении луча OX за точку O.

Требуется написать программу, которая по координатам вершин двух различных простых N-угольников определяет, существует ли гомотетия, переводящая первый многоугольник во второй и, если существует, вычисляет ее центр и коэффициент.

Входные данные

В первой строке входного файла содержится целое число n (3 ≤ n ≤ 1000) – количество вершин в каждом многоугольнике

В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин первого многоугольника в порядке обхода против часовой стрелки.

В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин второго многоугольника в порядке обхода против часовой стрелки.

Выходные данные

Если существует гомотетия, которая переводит первый многоугольник во второй, то необходимо вывести в первой строке выходного файла слово «YES», а во второй строке – три вещественных числа – координаты центра гомотетии и ее коэффициент, которые вычисляются с точностью не менее 10-5. Если искомой гомотетии не существует, необходимо вывести в выходной файл слово «NO».

Примеры
Входные данные
3
-1 1
1 1
1 5
1 9
-3 1
1 1
Выходные данные
YES
1.0 1.0 2.0
Входные данные
3
-1 1
1 1
1 5
1 1
0 0
1 0
Выходные данные
NO
#1152
Информатизация садоводства
  

Дачный участок Степана Петровича имеет форму прямоугольника размером a × b. На участке имеется n построек, причем основание каждой постройки — прямоугольник со сторонами, параллельными сторонам участка.

Вдохновленный успехами соседей, Степан Петрович хочет посадить на своем участке m видов плодовых культур (участок Степана Петровича находится в северной местности, поэтому m = 1 или m = 2). Для каждого вида растений Степан Петрович хочет выделить отдельную прямоугольную грядку со сторонами, параллельными сторонам участка. Само собой, грядки не могут занимать территорию, занятую постройками или другими грядками.

Степан Петрович хочет расположить грядки таким образом, чтобы их суммарная площадь была максимальной. Грядки не должны пересекаться, но могут касаться друг друга.


грядка №1



дом

сарай

грядка №2


Требуется написать программу, которая по заданным размерам участка и координатам построек определяет оптимальное расположение планируемых грядок.

Входные данные

В первой строке входного файла содержатся два целых числа n и m (0 ≤ n ≤ 10; 1 ≤ m ≤ 2).

Во второй строке содержатся два целых числа a и b (1 ≤ a, b ≤ 10000).

Далее следуют n строк, каждая из которых содержит четыре целых числа xi,1 , yi,1, xi,2, yi,2 –координаты двух противоположных углов постройки (0 xi,1 < xi,2 a, 0 yi,1 < yi,2   b). Различные постройки не могут пересекаться, но могут касаться друг друга.

Выходные данные

В выходной файл необходимо вывести m строк, каждая из которых содержит координаты двух противоположных углов предполагаемой грядки. Координаты должны быть целыми (всегда можно добиться максимальной суммарной площади грядок, располагая их в прямоугольниках с целыми координатами).

В случае, если в вашем решении Степану Петровичу следует расположить менее m грядок, необходимо вывести для грядок, которые не следует сажать, строку «0 0 0 0» (см. второй пример ниже).

Примеры
Входные данные
2 2
7 5
4 2 6 4
0 1 2 2
Выходные данные
0 2 4 5
2 0 7 2
Входные данные
3 2
4 4
0 0 4 1
0 1 1 4
3 1 4 4
Выходные данные
1 1 3 4
0 0 0 0
Страница: << 35 36 37 38 39 40 41 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест