#3296

Поход (6-9)

Темы: [Динамическое программирование: два параметра]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 6-9 классы, 2011, Задача D ]

Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.

Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.

Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.

Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.

Входные данные

Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит \(200\) символов.

Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.

Выходные данные

Выведите одно целое число - минимальное количество переправ.

Примечание

Рисунок к приведенному выше примеру.

Примеры

Входные данные

LLBLRRBRL

Выходные данные

#3297

Поход (10-11)

Темы: [Динамическое программирование: один параметр]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2011, Задача D ]

Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.

Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.

Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.

Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.

Входные данные

Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит \(10^5\) символов.

Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.

Выходные данные

Выведите одно целое число - минимальное количество переправ.

Примечания

Рисунок к приведенному выше примеру.

Примеры

Входные данные

LLBLRRBRL

Выходные данные

#3298

Футурама

Источники: [ Личные олимпиады, Московская олимпиада школьников, 6-9 классы, 2011, Задача E ] [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2011, Задача E ]

С помощью изобретенной профессором машины Фарнсворт и Эми меняются телами с целью осуществить свои мечты: профессор жаждет острых ощущений, а Эми мечтает есть от пуза, не опасаясь за фигуру. Впоследствии выясняется, что обмен разумом между двумя телами возможен не более одного раза, и чтобы вернуться обратно в свои тела нужно произвести промежуточный обмен. Бендер предлагает свою помощь, однако, заполучив тело Эми, он тут же скрывается, чтобы под чужой личиной украсть корону императора Робо-Венгрии.
Эми, недовольная возможностями профессорского тела в плане обжорства, уговаривает поменяться Лилу. Фрай приходит в ужас. Лила обижена и обвиняет Фрая в том, что его заботит только ее внешность. Фрай в отместку меняется телами с Зойдбергом.
Бендер оказывается пойман при попытке ограбления, однако освобождается, убедив императора в том, что он - робот в теле человека. Узнав, что император втайне мечтает пожить немного жизнью простых людей, Бендер предлагает тому на время поменяться телами. Но так как Профессор уехал рисковать жизнью в теле Бендера, пришлось подсунуть императору вместо своего корпуса автоматизированное помойное ведро.
Фрай в теле Зойдберга и Лила в теле Профессора встречаются в ресторане, чтобы выяснить отношения. В конце концов они понимают, что любят друг друга вовсе не за внешность. При виде сцены их бурного примирения Эми, на этот раз уже в теле Гермеса, надолго теряет аппетит.
Бендер, поменявшись телами с правителем Робо-Венгрии, наслаждается жизнью на его яхте. Однако именно в этот вечер заговорщики совершают покушение на императора. Жизнь Бендеру спасает появление профессора Фарнсворта.
После того, как все герои решают свои личные проблемы, профессору с помощью Бубльгума Тэйта и Сладкого Клайда из команды "Ударники" удается вернуть всех в свои тела.

"Футурама". Десятый эпизод шестого сезона.

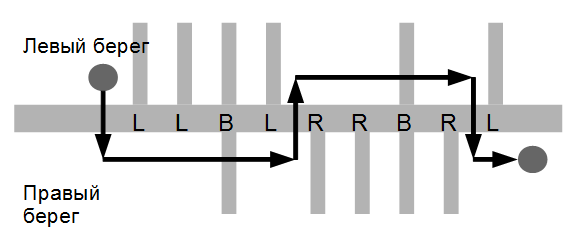
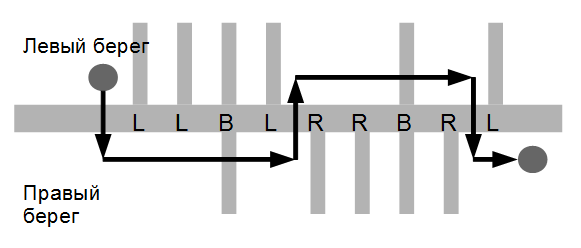
В очередной серии Футурамы было проведено несколько обменов разумами между телами героев,но, по крайней мере Бубльгум Тэйт и Сладкий Клайд в обменах не участвовали. Теперь необходимо вернутьразумы всех героев в свои тела. К сожалению, два тела могут участвовать только в одном обмене,поэтому обратные обмены для этого произвести невозможно. Например, если тело 1поменялось разумом с телом 2, а потом тело 1 поменялось разумом с телом 3,то в теле 1 находится разум третьего героя, в теле 2 - разум первого героя,а в теле 3 - второго.Теперь можно произвести обмен разумами только между телами 2 и 3, тогда разум второго героявернется в свое тело, а первому и третьему героям могут помочь только Тэйт с Клайдом.

Помогите героям Футурамы вернуться в свои тела.

Входные данные

Во входном файле записаны целые числа \(N\) (\(4\leq N\leq 20\)) и \(M\)(\(1\leq M\leq 100\)) - количество героев Футурамы и количество произведенных обменов разумами.Герои занумерованы числами от \(1\) до \(N\), изначально разум каждого из героев находится в своем теле. В последующих \(M\) строчках записана последовательность совершенных обменов разумами. Каждый обмен описывается двумя различными числами - номерами тел, которые, в этом обмене меняются разумами. Бубльгум Тэйт и Сладкий Клайд, как наиболее разумные герои, имеют номера \(N-1\) и \(N\), и гарантируется, что в исходных обменах они не участвовали.

Решения, верно работающие в случаях, когда каждое тело участвовало в обмене не больше одного раза будут набирать не менее 40 баллов.

Выходные данные

Выведите план обменов для возвращения разумов героев в свои телав виде пар различных чисел - номеров тел которые участвовали в соответствующем обмене.Причем никакие два тела не должны обмениваться между собой разумами более одного раза,включая исходные обмены. Если обменов не требуется, то можно ничего не выводить.Если планов обменов несколько, то выведите любой из них (не обязательно минимальный).

Вернуть разумы героев в свои тела всегда возможно.

Примечание

Приведем таблицу положения героев в телах после каждого из обменов:

Обмен	Тело 1	Тело 2	Тело 3	Тело 4
До обменов	1	2	3	4
1-2	2	1	3	4
1-3	3	1	2	4
2-4	3	4	2	1
1-4	1	4	2	3
2-3	1	2	4	3
3-4	1	2	3	4

Примеры

Входные данные

4 1
1 2

Выходные данные

#3302

Type Printer

Темы: [Бор]

Источники: [ Личные олимпиады, Международные олимпиады, 2008, Задача A ]

Вам нужно напечатать \(N\) слов на Movable Type Printer. Movable Type Printers — это старые принтеры, для работы которых требуется ставить маленькие металлические кусочки (каждый из кусочков содержит одну букву) в определенном порядке, образуя таким образом слова. Потом все они вдавливаются в лист бумаги. Таким образом печатается одно слово. Ваш принтер позволяет делать следующие операции:

Добавить букву в конец слова, находящегося сейчас на принтере.
Удалить последнюю букву из слова, находящегося сейчас на принтере. Эту операцию можно делать, только если слово содержит хотя бы одну букву.
Напечатать слово, находящееся на принтере (при этом слово никуда не исчезает, можно печатать его ещё раз и ещё раз).

Изначально на принтере содержится пустое слово. В конце печати на принтере можно оставить непустое слово. Слова, которые вам даны, вы можете печатать в произвольном порядке.

Каждая из трёх операций занимает одну единицу времени. Вам нужно найти последовательность операций, которая печатает данные \(N\) слов за минимальное время. Если минимальных последовательностaей несколько, выведите любую.

Входные данные

Ваша программа должна считать следующие входные данные:

На первой строке число \(N\) (\(1 \le N \le 25\,000\)).
На следующих \(N\) строках слова, состоящие из маленьких букв латинского алфавита. Длина каждого слова не превышает 20. Все слова различны.

Выходные данные

Ваша программа должна вывести следующие данные:

На первой строке \(M\) — число операций.
На следующих \(M\) строках по одному символу — описание операций. Каждая операция описывается одним символом:
- Добавление символа обозначается собственно символом.
- Удаление символа обозначается символом «-» (минус, ASCII-код 45).
- Операция «напечатать текущее слово» обозначается символом «P» (заглавная латинская буква P).

Примеры

Входные данные

3
print
the
poem

Выходные данные

20
t
h
e
P
-
-
-
p
o
e
m
P
-
-
-
r
i
n
t
P

#3303

Islands

Источники: [ Личные олимпиады, Международные олимпиады, 2008, Задача B ]

Вы гуляете в парке, где есть \(N\) островов. Когда-то с каждого острова \(i\) перекинули по одному мосту длиной \(L_i\). Всего мостов в парке \(N\). Несмотря на то, что мосты строились по направлению от одного острова к другому, сейчас по ним можно ходить в любом направлении. Также между каждой парой островов ходит паром.

Гулять вам нравится больше, чем кататься на паромах, поэтому вы решили максимизировать суммарную длину мостов, по которым вы пройдёте, соблюдая следующие ограничения:

Можно начать путь на любом острове.
Нельзя посетить остров дважды.
В любой момент можно отправиться с текущего острова \(S\) на другой, ранее не посещённый остров \(D\). Можно добраться с \(S\) на \(D\):
- Пешком, если между этими островами есть мост. В таком случае длина этого моста добавляется к суммарной длине пройденных мостов.
- Паромом. Этот вариант можно выбрать, только если \(D\) недостижим из \(S\) по любой комбинации мостов и/или уже использованных паромов. (При проверке достижимости рассматриваются все пути, включая проходящие уже посещённые острова.)

Заметьте, что необязательно посещать все острова и может оказаться невозможно пройти все мосты.

Даны описания мостов. Найдите максимальное расстояние, которое можно пройти по указанным правилам.

Входные данные

Первая строка ввода содержит единственное целое число \(N\) — количество островов в парке (\(2 \le N \le 1\,000\,000\)). Острова нумеруются целыми числами от \(1\) до \(N\).

Каждая из следующих \(N\) строк описывает мост. \(i\)-я строка описывает мост, ведущий с острова \(i\) двумя целыми числами: первое из них задаёт номер острова, с которым мост соединяет \(i\)-й остров, второе — длину \(L_i\) этого моста. Длина — натуральное число, не превышающее \(100\,000\,000\).

Выходные данные

Выведите одну строку, содержащую единственное целое число — максимальное возможное расстояние, которое можно пройти по мостам.

Примечание к примеру тестов

\(N = 7\) мостов в примере таковы: \((1-3)\), \((2-7)\), \((3-4)\), \((4-1)\), \((5-1)\), \((6-3)\) и \((7-2)\). Заметьте, что два различных моста соединяют острова 2 и 7.

Один из способов получить максимальное расстояние таков:

Начать с острова 5.
Пройти по мосту длины 9 и оказаться на острове 1.
Пройти по мосту длины 8 и оказаться на острове 3.
Пройти по мосту длины 4 и оказаться на острове 6.
Переправиться на пароме на остров 7.
Пройти по мосту длины 3 и оказаться на острове 2.

В конце вы окажетесь на острове 2, и суммарное расстояние будет равно \(9+8+4+3 = 24\). Единственный остров, оставшийся непосещённым, — 4. Заметьте, что по окончании описанного путешествия ни один остров больше посетить нельзя. Более точно:

Нельзя отправиться туда пешком, так как нет моста, соединяющего 2 (текущий остров) и 4.
Нельзя воспользоваться паромом, так как 4 достижим из 2, где вы теперь находитесь. Способ его достичь: воспользоваться мостом \((2-7)\), затем переправиться на пароме, которым вы уже переправлялись с острова 7 на остров 6, затем мост \((6-3)\) и, наконец, мост \((3-4)\).

Примеры

Входные данные

Выходные данные