Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
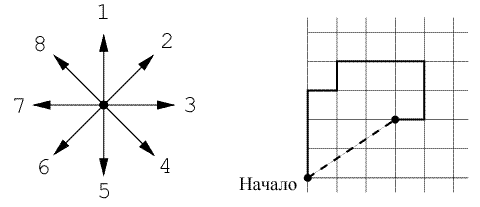
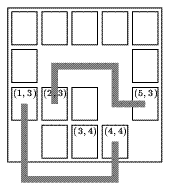
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 405 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 13 14 15 16 17 18 19 >> Отображать по:
#1005
Домой на электричках
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Одна из команд-участниц олимпиады решила вернуться домой на электричках. При этом ребята хотят попасть домой как можно раньше. К сожалению, не все электрички идут от города, где проводится олимпиада, до станции, на которой живут ребята. И, что еще более обидно, не все электрички, которые идут мимо их станции, останавливаются на ней (равно как вообще, электрички останавливаются далеко не на всех станциях, мимо которых они идут)

Все станции на линии пронумерованы числами от 1 до N. При этом станция номер 1 находится в городе, где проводится олимпиада, и в момент времени 0 ребята приходят на станцию. Станция, на которую нужно попасть ребятам, имеет номер E.

Напишите программу, которая по данному расписанию движения электричек вычисляет минимальное время, когда ребята могут оказаться дома.

Входные данные

Во входном файле записаны сначала числа N (\(2 \le N \le 100\)) и E (\(2 \le E \le N\)). Затем записано число M (\(0 \le M \le 100\)), обозначающее число рейсов электричек. Далее идет описание M рейсов электричек. Описание каждого рейса электрички начинается с числа Ki (\(2 \le K \le N\)) — количества станций, на которых она останавливается, а далее следует Ki пар чисел, первое число каждой пары задает номер станции, второе — время, когда электричка останавливается на этой станции (время выражается целым числом из диапазона от 0 до 109). Станции внутри одного рейса упорядочены в порядке возрастания времени. В течение одного рейса электричка все время движется в одном направлении — либо от города, либо к городу.

Выходные данные

В выходной файл выведите одно число — минимальное время, когда ребята смогут оказаться на своей станции. Если существующими рейсами электричек они добраться не смогут, выведите –1.

Примеры
Входные данные
5 2
2
4 1 1 3 2 4 10 5 20
3 5 10 4 15 2 40
Выходные данные
40
#1006
Клад
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Найти закопанный пиратами клад просто: всё, что для этого нужно – это карта. Как известно, пираты обычно рисуют карты от руки и описывают алгоритм нахождения клада так: «Встаньте около одинокой пальмы. Пройдите тридцать шагов в сторону леса, потом семнадцать шагов в сторону озера, …, наконец десять шагов в сторону большого булыжника. Клад находится под ним». Большая часть таких указаний просто сводится к прохождению какого-то количества шагов в одном из восьми направлений (1 – север, 2 – северо-восток, 3 – восток, 4 – юго-восток, 5 – юг, 6 – юго-запад, 7 – запад, 8 – северо-запад) (см. рис). Длина шага в любом направлении равна 1.

Путешествие по такому пути обычно является прекрасным способом посмотреть окрестности, однако в наше время постоянной спешки ни у кого нет времени на это. Поэтому кладоискатели хотят идти напрямую в точку, где зарыт клад. Например, вместо того, чтобы проходить три шага на север, один шаг на восток, один шаг на север, три шага на восток, два шага на юг и один шаг на запад, можно пройти напрямую, использовав около 3.6 шага (см. рис).


 

Вам необходимо написать программу, которая по указаниям пиратов определяет точку, где зарыт клад.

Входные данные

Первая строка входного файла содержит число N – число указаний (1≤N≤40). Последующие N строк содержат сами указания – номер направления (целое число от 1 до 8) и количество шагов (целое число от 1 до 1000). Числа разделены пробелами.

Выходные данные

В выходной файл выведите координаты X и Y точки (два вещественных числа, разделённые пробелом), где зарыт клад, считая, что ось Ox направлена на восток, а ось Oy – на север. В начале кладоискатель должен стоять в начале координат. Координаты необходимо вывести с погрешностью не более 10-3.

Примеры
Входные данные
6
1 3
3 1
1 1
3 3
5 2
7 1
Выходные данные
3.000 2.000
Входные данные
1
8 10
Выходные данные
-7.071 7.071
#1008
Целые точки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
32 megabytes

Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).

Входные данные

В первой строке содержится N (3≤N≤1000) – число вершин многоуголь­ника. В последующихN строках идут координаты (Xi, Yi) вершин многоугольника в порядке обхода по часовой стрелке.Xi и Yi - целые числа, по модулю не превосходящие 1000000.

Выходные данные

В выходной файл вывести одно число – искомое число точек.

Примеры
Входные данные
4
1 1
1 2
2 2
2 1
Выходные данные
0
Входные данные
3
0 0
6 2
4 0
Выходные данные
1
#1009
Степень
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
32 megabytes
По заданному числа A необходимо найти минимальное N, такое, что N^N кратно A

Для того чтобы проверить, как её ученики умеют считать, Мария Ивановна каждый год задаёт им на дом одну и ту же задачу – для заданного натурального A найти минимальное натуральное N такое, что N в степени N (N, умноженное на себя N раз) делится на A. От года к году и от ученика к ученику меняется только число A.

Вы решили помочь будущим поколениям. Для этого вам необходимо написать программу, решающую эту задачу.

Входные данные

Во входном файле содержится единственное число A (1 ≤ A ≤ \(10^9\) – на всякий случай; вдруг Мария Ивановна задаст большое число, чтобы «завалить» кого-нибудь…).

Выходные данные

В выходной файл вывести единственное число N.

Примеры
Входные данные
1
Выходные данные
1
Входные данные
8
Выходные данные
4
#1010
Игра с фишками
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
32 megabytes
Задан лабиринт и пары клеток. Требуется определить, существует ли путь между парами.

Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).

Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:

  1. Путь должен состоять из отрезков вертикальных и горизонтальных прямых.
  2. Путь не должен пересекать других фишек.

При этом часть пути может оказаться вне доски. Например:

 

Фишки с координатами (1,3) и (4,4) могут быть соединены. Фишки с координатами (2,3) и (5,3) тоже могут быть соединены. А вот фишки с координатами (2,3) и (3,4) соединить нельзя – любой соединяющий их путь пересекает другие фишки.

Вам необходимо написать программу, проверяющую, можно ли соединить две фишки путем, обладающим вышеуказанными свойствами, и, в случае положительного ответа, определяющую минимальную длину такого пути (считается, что путь имеет изломы, начало и конец только в центрах клеток (или «мнимых клеток», расположенных вне доски), а отрезок, соединяющий центры двух соседних клеток, имеет длину 1).

Входные данные

Первая строка входного файла содержит два натуральных числа: W – ширина доски, H – высота доски (1≤W,H≤75). Следующие H строк содержат описание доски: каждая строка состоит ровно из W символов: символ «X» (заглавная английская буква «экс») обозначает фишку, символ «.» (точка) обозначает пустое место. Все остальные строки содержат описания запросов: каждый запрос состоит из четырёх натуральных чисел, разделённых пробелами – X1, Y1, X2, Y2, причём 1≤X1,X2≤W, 1≤Y1,Y2≤H. Здесь (X1, Y1) и (X2, Y2) – координаты фишек, которые требуется соединить (левая верхняя клетка имеет координаты (1,1)). Гарантируется, что эти координаты не будут совпадать (кроме последнего запроса; см. далее). Последняя строка содержит запрос, состоящий из четырёх чисел 0; этот запрос обрабатывать не надо. Количество запросов не превосходит 20.

Выходные данные

Для каждого запроса необходимо вывести одно целое число на отдельной строке – длину кратчайшего пути, или 0, если такого пути не существует.

Примеры
Входные данные
5 4
XXXXX
X...X
XXX.X
.XXX.
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
Выходные данные
5
6
0
Входные данные
4 4
XXXX
XXXX
XXXX
XXXX
1 1 2 1
2 2 3 2
1 1 3 1
3 4 4 3
2 1 2 4
1 1 2 2
0 0 0 0
Выходные данные
1
1
4
6
11
0
Страница: << 13 14 15 16 17 18 19 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест