Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 405 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 30 31 32 33 34 35 36 >> Отображать по:
#1340
Легкоатлетический манеж МГУ
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).

Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.

Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.

Входные данные

Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).

Выходные данные

В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».

В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.


В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.

Примеры входных и выходных данных

Ввод

Вывод

2 4

YES

2 1 4

2 3 2

3 4

NO


#1341
Граффити на заборе
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Около прямолинейного забора, состоящего из N одинаковых бетонных плит, проводится конкурс граффити, в котором участвуют M граффити-художников. Художники должны разрисовать все плиты своими произведениями за наименьшее возможное время.

Плиты пронумерованы числами от 1 до N, граффити-художники имеют номера от 1 до M. Первоначально i-й граффити-художник находится около плиты с заданным номером pi. Каждому художнику требуется b минут на разрисовывание любой плиты. Каждую плиту должен разрисовать ровно один граффити-художник.

В начале работы, а также после разрисовывания любой плиты граффити-художник может перейти к любой неразрисованной плите. Время перемещения граффити-художника от любой плиты к соседней с ней одинаково и равно a минут. Таким образом, чтобы перейти от плиты с номером i к плите с номером j художнику требуется a×|i – j| минут.

Требуется написать программу, которая поможет участникам конкурса разрисовать все плиты за минимальное возможное время.

Входные данные

В первой строке входного файла указаны числа N — количество плит в заборе и M — количество граффити-художников (1 ≤ N, M ≤ 100000). Во второй строке заданы два целых числа: a — количество минут, которое требуется для перехода от любой плиты к соседней, и b — количество минут, которое требуется граффити-художнику на разрисовывание одной плиты (1 ≤ a, b ≤ 106). В третьей строке заданы M чисел p1, p2, …, pM — начальные положения граффити-художников (1 ≤ pi ≤ N).

Выходные данные

В первую строку выходного файла выведите минимальное количество минут, требуемых художникам для выполнения работы.

В последующих M строках выведите описание действий художников. В i-й из этих строк должно содержаться описание действий i-го художника: количество плит, которые должен разрисовать этот художник, и номера этих плит в очередности их разрисовывания. Если оптимальных решений несколько, можно вывести любое из них.

Примечание

Решения, корректно работающие при M ≤ 2, будут оцениваться из 40 баллов.

Примеры
Входные данные
10 2
19 56
9 2
Выходные данные
375
5 10 9 8 7 6 
5 1 2 3 4 5
#1342
Стековый калькулятор
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В кабинете информатики есть старый стековый калькулятор. Он содержит K ячеек памяти, организованных в виде стека. Первая ячейка называется вершиной стека. На индикаторе калькулятора отображается содержимое вершины стека, если стек непуст.

Над стеком может выполняться операция проталкивания. Применение этой операции приводит к записи числа на вершину стека. Перед этим, если в стеке уже были числа, то каждое из них перемещается в ячейку с номером на единицу больше. Если в стеке уже находится K чисел, то выполнение операции проталкивания невозможно.

Калькулятор позволяет выполнять арифметические операции. Они применяются к числам, хранящимся во второй и первой ячейках стека. Результат операции записывается в первую ячейку стека, а число из второй ячейки удаляется. После этого, если третья ячейка непуста, то число из неё переписывается во вторую, если есть число в четвертой ячейке — оно переписывается в третью и так далее до последней занятой ячейки, которая становится пустой. Для выполнения арифметической операции в стеке должно быть хотя бы два числа. Например, при выполнении операций сложения или умножения, значения соответственно суммы или произведения чисел из первой и второй ячеек помещаются на вершину стека. Операция вычитания выполняется так: из содержимого второй ячейки стека вычитается содержимое первой ячейки.

Известно, что калькулятор неисправен. Из цифровых клавиш работает только клавиша «1». Нажатие этой клавиши приводит к проталкиванию в стек числа 1. Например, попытка набрать число 11, два раза нажав клавишу «1», приводит к тому, что в стек два раза проталкивается число 1. Из операций работают только сложение (клавиша «+»), умножение (клавиша «*») и вычитание (клавиша «-»). Если в результате вычитания получено отрицательное число, то калькулятор зависает.

Легко заметить, что на индикаторе возможно получить произвольное натуральное число. Например, чтобы получить число 3, необходимо дважды нажать клавишу «1», затем клавишу «+» (на индикаторе после этого появится число 2), затем один раз нажать клавишу «1» и один раз — клавишу «+». При K > 2 того же результата можно достичь иначе, трижды нажав клавишу «1», а затем два раза клавишу «+». Дополнительно используя операции умножения и вычитания, в некоторых случаях число N можно получить быстрее, чем сложив N единиц.

Требуется написать программу, которая определяет, каким образом можно получить на индикаторе калькулятора заданное число N, выполнив минимальное количество нажатий клавиш. Стек изначально пуст.

Входные данные

В единственной строке входного файла записаны два натуральных числа — N и K (1 ≤ N ≤ 109, 2 ≤ K ≤ 100).

Выходные данные

В первой строке выходного файла выведите минимальное количество нажатий клавиш, необходимых для получения числа N. Если число нажатий не превосходит 200, то дополнительно выведите во второй строке оптимальную последовательность нажатий, приводящих к появлению данного числа на индикаторе.

Последовательность необходимо выводить без пробелов. Клавиши обозначаются символами «1» — протолкнуть число 1 в стек, «+» — выполнить операцию сложения, «*» — выполнить операцию умножения, «-» — вычесть из значения второй ячейки стека значение первой ячейки.

В результате выполнения выведенной последовательности нажатий на индикаторе должно отображаться число N. Если оптимальных последовательностей нажатий несколько, разрешается выводить любую из них.

Примечания

Решения, корректно работающие при N ≤ 100 и K ≤ 10, будут оцениваться из 40 баллов.

Решения, корректно работающие при N ≤ 106 и K ≤ 100, будут оцениваться из 80 баллов.

Примеры
Входные данные
1 2
Выходные данные
1
1
Входные данные
9 3
Выходные данные
11
11+1+11+1+*
#1344
Многоугольники
  
ограничение по времени на тест
0.1 second;
ограничение по памяти на тест
64 megabytes

На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:

  • никакие два многоугольника не имеют общих точек;
  • для каждого i –го многоугольника существует Pi многоугольников, внутри которых он находится, и N-1-Pi многоугольников, которые находятся внутри его, 0 ≤Pi≤N-1.

Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.

Входные данные

Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число Ci — количество вершин многоугольника, 3≤Ci≤20. Последующие Ci пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.

Выходные данные

Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть Pi — количество многоугольников, внутри которых находится i–ый многоугольник.

Примеры
Входные данные
3
3 -2 1 8 9 12 1
3 7 5 6 3 7 4
4 4 3 7 7 9 3 1 2
Выходные данные
0 2 1
#1346
ВТО
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

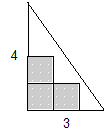Территория Великой Треугольной Области (ВТО) представляет собой прямоугольный треугольник. Длины его катетов равны M и N государственных единиц длины (ГЕД). Правительство ВТО решило покрыть как можно большую часть территории области квадратными плитами размером 11 ГЕД. Плиты должны плотно прилегать друг к другу и к катетам ВТО. Разрезать плиты нельзя.

Согласно межгосударственным соглашениям, правительство ВТО не имеет права покрыть частью своей плиты чужую территорию. Производитель поставляет плиты только контейнерными партиями — по P плит. Правительство заказывает столько контейнеров, сколько необходимо для реализации проекта.

Заведующий центральным складом, узнав про проект, решил, что его интересует коли­чество плит, которые останутся на складе из последнего контейнера после покрытия территории ВТО.

Напишите программу, которая по длинам катетов ВТО и вместимости контейнера находит количество плит, которые останутся на складе после осуществления проекта.

Входные данные

Единственная строка входного файла содержит три целых числа: M, N (2≤M, N≤2 000 000 000) и P (100≤P≤10 000).

Выходные данные

Единственная строка выходного файла должна содержать целое число — количество неиспользованных плит из последнего контейнера.

Примеры
Входные данные
4 3 100
Выходные данные
97
Страница: << 30 31 32 33 34 35 36 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест