Многие системы форматирования текста, например TEX или Wiki, используют для разбиения текста на абзацы пустые строки. Текст представляет собой последовательность слов, разделенных пробелами, символами перевода строк и следующими знаками препинания: «,», «.», «?», «!», «-», «:» и «’» (ASCII коды 44, 46, 63, 33, 45, 58, 39). Каждое слово в тексте состоит из заглавных и прописных букв латинского алфавита и цифр. Текст может состоять из нескольких абзацев. В этом случае соседние абзацы разделяются одной или несколькими пустыми строками. Перед первым абзацем и после последнего абзаца также могут идти одна или несколько пустых строк.

Дальнейшее использование исходного текста предполагает его форматирование, которое осуществляется следующим образом. Каждый абзац должен быть разбит на строки, каждая из которых имеет длину не больше \(w\). Первая строка каждого абзаца должна начинаться с отступа, состоящего из \(b\) пробелов. Слова внутри одной строки должны быть разделены ровно одним пробелом. Если после слова идет один или несколько знаков препинания, они должны следовать сразу после слова без дополнительных пробелов. Если очередное слово вместе со следующими за ним знаками препинания помещается на текущую строку, оно размещается на текущей строке. В противном случае, с этого слова начинается новая строка. В отформатированном тексте абзацы не должны разделяться пустыми строками. В конце строк не должно быть пробелов.

Требуется написать программу, которая по заданным числам \(w\) и \(b\) и заданному тексту выводит текст, отформатированный описанным выше образом.

Отделу космических исследований поступило задание сфотографировать из космоса \(n\) объектов в заданной области. Область имеет форму квадрата размером \(50\times 50\) километров. Если разделить ее на квадраты размером \(1\times 1\) километр, то интересующие отдел объекты окажутся в центрах некоторых единичных квадратов.

Введем систему координат, направив ось OX с запада на восток и ось OY с юга на север. Тогда каждому единичному квадрату будут сопоставлены координаты в диапазоне от 1 до 50, как показано на рисунке ниже.

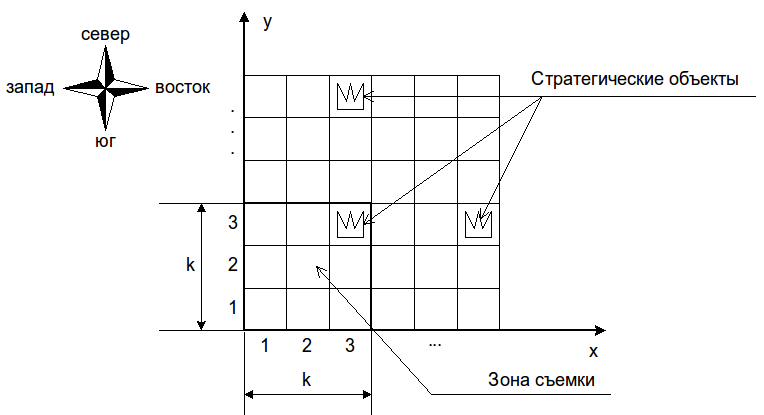
Для космической съемки используется специальный фотоаппарат высокого разрешения, установленный на космическом спутнике. Фотоаппарат может делать снимки квадратных участков земной поверхности размером \(k\times k\) километров. Исходно аппарат наведен на юго-западный угол заданной области, то есть, если сделать снимок, на нем будут видны единичные квадраты с координатами \(x\) и \(y\) от \(1\) до \(k\) километров.

С помощью специальных двигателей можно изменять орбиту спутника, что приводит к изменению участка съемки. За один день орбиту спутника можно изменить таким образом, что участок съемки сместится либо на один километр на запад, либо на один километр на восток, либо на один километр на север. Переместить участок съемки на юг невозможно. Непосредственно между перемещениями спутника можно сделать снимок, временем съемки можно пренебречь.

Руководство отдела заинтересовалось вопросом: за какое минимальное количество дней можно сделать снимки всех объектов заданной области.

Требуется написать программу, которая по заданному расположению объектов и размеру снимка \(k\) определит минимальное время, за которое можно сделать снимки всех объектов заданной области.

Параллель восьмых классов написала контрольную работу. В результате ровно A% учащихся получили 5, ровно B% — 4, ровно C% — 3, а остальные D% написали её на 2. Какое минимальное количество школьников должно быть в параллели восьмых классов для того, чтобы могли получиться такие результаты?

Этим летом у бабушки был большой урожай яблок. Она собрала яблоки в корзину и отдала своим \(K\) внукам.

Первый внук взял из корзины половину всех яблок и еще \(a_1\) яблоко (если количество яблок не делилось на два, то результат деления на два он мог округлить как в большую сторону, так и в меньшую). К примеру, если в корзине было 7 яблок и \(a_1 = 1\), то он мог взять либо 4, либо 5, а если было 6 яблок и \(a_1 = 1\), то он взял ровно 4.

Второй внук взял половину от всех оставшихся яблок и ещё \(a_2\) (если яблок было нечетное количество, то он также мог округлить половину как в большую, так и в меньшую сторону). И так далее, \(K\)-ый внук взял половину яблок, оставшихся после \(K - 1\) внука, и ещё \(a_k\). В итоге в корзине ничего не осталось.

Теперь они задумались, насколько же большой урожай был у бабушки. Ни один из них не помнит, делилось ли количество яблок на 2 нацело при его выборе, а если нет, то в какую сторону он округлил половину яблок. Внуков интересует минимальное и максимальное изначальное количество яблок в корзине, при которых могли произойти описанные события.