Встретились однажды три культорга ЛКШ...
Вам известна скобочная последовательность, записанная первым культоргом. Найдите число, которое произнёс третий культорг.
Циклическим сдвигом строки называется перенос некоторого (возможно, нулевого) количества символов из конца строки в её начало без изменения их порядка.
В единственной строке дана скобочная последовательность, записанная первым культоргом. Длина последовательности не равна нулю и не превышает \(100\,000\) символов.
Выведите количество циклических сдвигов, превращающих записанную скобочную последовательность в правильную.
)(()
1
)()(
2
()
1
У мальчика Васи есть \(N\) шоколадок (возможно, разного веса). Вася пригласил к себе в гости \(K\) своих друзей и хочет подарить им шоколадки. Чтобы никому из друзей не было обидно, Вася решил раздать шоколадки так, чтобы каждому другу досталось одно и то же количество шоколада (т.е. суммарный вес шоколадок, доставшихся каждому другу, должен быть одинаковым). Вася может раздать все свои шоколадки, может раздать лишь часть, но, поскольку он — очень гостеприимный мальчик, он не хочет оставлять друзей совсем без шоколада (т.е. сумма весов шоколадок, доставшихся каждому другу, должна быть строго положительной). Все шоколадки красиво упакованы, т.е. делить их на части нельзя.
Определите, сколько у Васи есть способов раздать шоколад своим друзьям. Два способа считайте различными тогда и только тогда, когда существует шоколадка, которая в одном способе досталась некоторому другу, а в другом — другому другу или вовсе не была отдана друзьям.
В первой строке входного файла находятся два натуральных числа \(N\) и \(K\) (\(1 \leq N \leq 15\), \(1 \leq K \leq 15\)) — количество шоколадок у Васи и количество друзей, которых Вася пригласил в гости. Во второй строке содержатся \(N\) натуральных чисел — веса шоколадок. Ни один из весов не превосходит \(1000\).
Выведите в выходной файл одно число — количество способов раздать шоколадки друзьям.
Во втором примере возможные распределения шоколадок следующие:
5 4 1 2 1 1 1
24
3 2 1 1 2
4
Маленький Вася очень любит поезда. На день рождения ему подарили игрушечную железную дорогу. В комплект к железной дороге входит поезд, состоящий из \(n\) вагонов, пронумерованных числами от 1 до \(n\).
Любимым занятием Васи стала сортировка поездов с использованием специального сортировочного тупика.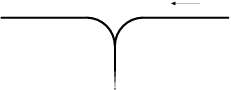
Справа к тупику подъезжает поезд, составленный из всех \(n\) вагонов. Затем вагоны по одному загоняются в сортировочный тупик и выгоняются из него налево. Васе нравится, если ему удается отсортировать поезд с помощью сортировочного тупика — добиться того, чтобы слева от тупика вагоны были расположены по порядку от 1 до \(n\).
Например, пусть в исходном поезде 4 вагона, которые следуют в порядке 3, 1, 2, 4. Его можно отсортировать следующим образом. Загоняем вагон 3 в тупик. Загоняем вагон 1 в тупик. Выгоняем вагон 1 из тупика. Загоняем вагон 2 в тупик. Выгоняем вагон 2 из тупика. Выгоняем вагон 3 из тупика. Загоняем вагон 4 в тупик. Выгоняем вагон 4 из тупика.
Не все поезда можно отсортировать таким образом. Например, поезд из 3 вагонов, следующих в порядке 2, 3, 1, отсортировать нельзя.
Вася выписал на листке в лексикографическом порядке все поезда длины \(n\), которые можно отсортировать с помощью тупика. Поезд \((a_1, a_2, \ldots, a_n)\) идет раньше поезда \((b_1, b_2, \ldots, b_n)\) в лексикографическом порядке, если существует такое \(i\) (\(1 \le i \le n\)), что для всех \(j < i\) выполняется \(a_j = b_j\), а \(a_i < b_i\). Например, все поезда из трех вагонов, которые можно отсортировать с помощью тупика, в лексикографическом порядке выписываются следующим образом: \((1, 2, 3)\), \((1, 3, 2)\), \((2, 1, 3)\), \((3, 1, 2\)), \((3, 2, 1)\).
Вася потерял свой листок, и его интересует вопрос: какой поезд был выписан на его листке под номером \(k\). Помогите ему выяснить это.
Входной файл содержит два целых числа — \(n\) и \(k\) (\(1 \le n \le 30\), \(1 \le k \le 10^{18}\)).
Выведите в выходной файл \(n\) целых чисел: \(k\)-й в лексикографическом порядке поезд из \(n\) вагонов, который можно отсортировать с помощью тупика.
Если с помощью тупика можно отсортировать менее \(k\) поездов из \(n\) вагонов, выведите \(-1\).
4 1
1 2 3 4
4 3
1 3 2 4
4 15
-1
Ваш младший брат Петя недавно получил домашнее задание и ему нужна ваша помощь. Учитель дал ему последовательность чисел, которую требуется отсортировать в возрастающем порядке. Во время сортировки можно менять местами два любых числа. Каждый обмен имеет стоимость, равную сумме чисел, которые в него входят.
Напишите программу, которая найдет минимальную стоимость такой сортировки заданной последовательности.
Входной файл содержит две строки. Первая строка содержит положительное целое число n (1000 > n > 1) — количество чисел, которые требуется отсортировать. Вторая строка содержит n различных чисел (каждое положительное и не больше 1000), которые надо отсортировать.
Выведите одну строку, содержащую минимальную стоимость сортировки чисел как показано в примере.
3 3 2 1
4
4 8 1 2 4
17
5 1 8 9 7 6
41
6 8 4 5 3 2 7
34