Развлекательный телеканал транслирует шоу «Колесо Фортуны». В процессе игры участники шоу крутят большое колесо, разделенное на сектора. В каждом секторе этого колеса записано число. После того как колесо останавливается, специальная стрелка указывает на один из секторов. Число в этом секторе определяет выигрыш игрока.

Юный участник шоу заметил, что колесо в процессе вращения замедляется из-за того, что стрелка задевает за выступы на колесе, находящиеся между секторами. Если колесо вращается с угловой скоростью \(v\) градусов в секунду, и стрелка, переходя из сектора \(X\) к следующему сектору, задевает за очередной выступ, то текущая угловая скорость движения колеса уменьшается на \(k\) градусов в секунду. При этом если \(v \le k\), то колесо не может преодолеть препятствие и останавливается. Стрелка в этом случае будет указывать на сектор \(X\).

Юный участник шоу собирается вращать колесо. Зная порядок секторов на колесе, он хочет заставить колесо вращаться с такой начальной скоростью, чтобы после остановки колеса стрелка указала на как можно большее число. Колесо можно вращать в любом направлении и придавать ему начальную угловую скорость от \(a\) до \(b\) градусов в секунду.

Требуется написать программу, которая по заданному расположению чисел в секторах, минимальной и максимальной начальной угловой скорости вращения колеса и величине замедления колеса при переходе через границу секторов вычисляет максимальный выигрыш.

Победитель школьного этапа олимпиады по информатике нашел дома в старых бумагах результаты чемпионата страны по стрельбе из лука, в котором участвовал его папа. К сожалению, листок с результатами сильно пострадал от времени, и разобрать фамилии участников было невозможно. Остались только набранные каждым участником очки, причем расположились они в том порядке, в котором участники чемпионата выполняли стрельбу.

Расспросив папу, школьник выяснил, что количество очков, которое набрал папа, заканчивается на 5, один из победителей чемпионата стрелял раньше, а папин друг, который стрелял сразу после папы, набрал меньше очков. Теперь он заинтересовался, какое самое высокое место мог занять его папа на том чемпионате.

Будем считать, что участник соревнования занял \(k\)-е место, если ровно \((k - 1)\) участников чемпионата набрали строго больше очков, чем он. При этом победителями считались все участники чемпионата, занявшие первое место.

Требуется написать программу, которая по заданным результатам чемпионата определяет, какое самое высокое место на чемпионате мог занять папа победителя школьного этапа олимпиады по информатике.

Министерство дорожного транспорта решило построить себе новый офис. Поскольку министр регулярно выезжает с инспекцией наиболее важных трасс, было решено, что офис министерства не должен располагаться слишком далеко от них.

Наиболее важные трассы представляют собой прямые на плоскости. Министерство хочет выбрать такое расположение для своего офиса, чтобы максимум из расстояний от офиса до трасс был как можно меньше.

Требуется написать программу, которая по заданному расположению наиболее важных трасс определяет оптимальное расположение дома для офиса министерства дорожного транспорта.

На планете Плюк открылся новый космический кегельбан. Поле для кегельбана представляет собой бесконечную плоскость, на которой расставлены кегли.

Каждая кегля представляет собой высокий цилиндр с основанием в виде круга радиусом r метров. Все кегли одинаковые. Кегли расставлены по следующим правилам. Кегли образуют n рядов, в первом ряду стоит одна кегля, во втором — две, и так далее. В последнем n-м ряду стоит n кеглей. Введем на плоскости систему координат таким образом, чтобы единица измерения была равна одному километру. Центр единственной кегли в первом ряду находится в точке (0, 0). Центры кеглей во втором ряду находятся в точках (–1, 1) и (1, 1). Таким образом, центры кеглей в i-м ряду находятся в точках с координатами (–(i – 1), i –  1), (–( i – 3), i – 1), …, (i – 1, i – 1).

Игра происходит следующим образом. Используется шар с радиусом q метров. Игрок выбирает начальное положение центра шара (x_c,  y_c) и вектор направления движения шара (v_x, v_y). После этого шар помещается в начальную точку и двигается, не останавливаясь, в направлении вектора (v_x, v_y). Считается, что шар сбил кеглю, если в процессе движения шара имеет место ситуация, когда у шара и кегли есть общая точка. Сбитые кегли не меняют направления движения шара и не сбивают соседние кегли при падении.

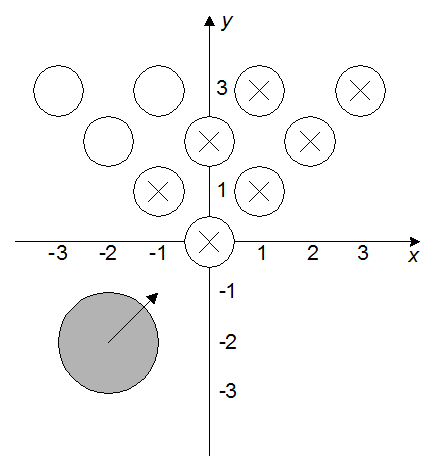
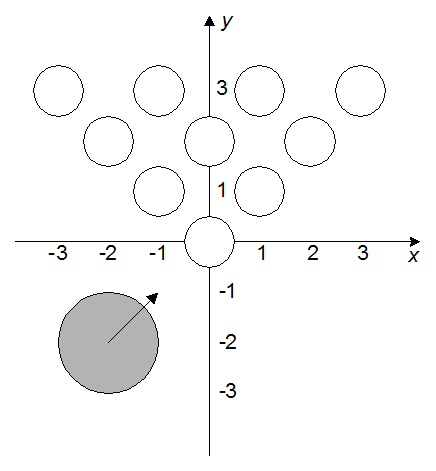
На рисунке приведен пример расположения кеглей для r = 500, n = 4 и шара для q = 1000, x_c = –2, y_c = –2, v_x = 1, v_y = 1.

Требуется написать программу, которая по заданным радиусу кегли r, количеству рядов кеглей n, радиусу шара q, его начальному положению ( x_c, y_c) и вектору направления движения (v_x,  v_y) определяет количество кеглей, сбитых шаром.

Строка s называется супрефиксом для строки t, если t начинается с s и заканчивается на s. Например, «abra» является супрефиксом для строки «abracadabra». В частности, сама строка t является своим супрефиксом. Супрефиксы играют важную роль в различных алгоритмах на строках.

В этой задаче требуется решить обратную задачу о поиске супрефикса, которая заключается в следующем. Задан словарь, содержащий n слов t₁, t₂, …, t_n и набор из m строк-образцов s₁, s₂, …, s_m. Необходимо для каждой строки-образца из заданного набора найти количество слов в словаре, для которых эта строка-образец является супрефиксом.

Требуется написать программу, которая по заданному числу n, n словам словаря t₁, t₂, …, t_n, заданному числу m и m строкам-образцам s₁, s₂, …, s_m вычислит для каждой строки-образца количество слов из словаря, для которых эта строка-образец является супрефиксом.