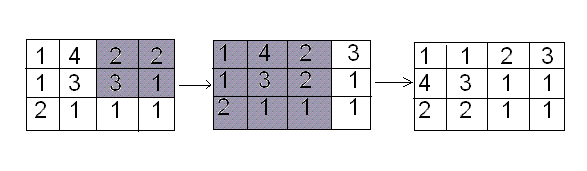Недавно археологической командой «Раскопай» были обнаружены остатки древней цивилизации. Особое внимание привлекла карта с месторасположением народов, живших в то время. Карта представляет собой прямоугольный лист, разлинованный горизонтальными линиями на M полос и вертикальными линиями на N столбцов. Таким образом формируются M*N клеток — древних поселений, которые заселялись сообществами. В каждой клетке этой карты написано натуральное число — идентификатор народа, к которому принадлежит это сообщество людей (рукопись с соответствием между идентификаторами и народами также была обнаружена).
<>Группа историков «Разузнай» имеет такую же карту, но только на тысячелетие древнее. Естественно, она может отличаться от той, которую нашли археологи — ведь за такой срок сообщества могли переселяться в другие поселения. Историками была высказана идея о механизме переселения народов.
Чтобы объяснить этот процесс введем систему координат на карте так, что границы карты параллельны осям координат. Пусть координаты (0,0) соответствуют самой верхней левой клетке, а (N–1, M–1) — самой нижней правой. Переселение народов проходит в несколько этапов. Опишем как проходит каждый этап.
Назовем квадратом множество всех поселений с координатами (x,y) такими, что x1≤x≤x2, y1≤y≤y2, где x2–x1=y2–y1. Соответственно клетка (x1,y1) является левой верхней клеткой квадрата, (x2,y2) —нижней правой.
На каждом этапе переселения переселяются сообщества внутри некоторого квадрата по следующему правилу. Если переселение происходит внутри квадрата, левой верхней клеткой которого является клетка (x1,y1), а правой нижней — (x2,y2), то сообщество, проживавшее в поселении с координатами (x,y) (x1≤x≤x2, y1≤y≤y2) переселяется в поселение с координатами (x2–(y2–y),y2–(x2–x)), при этом, возможно, что некоторые сообщества остаются на своих местах. Все сообщества, живущие вне квадрата, в котором происходит переселение, остаются на своих местах.
Историки из «Разузнай» хотят для подтверждения (или опровержения) своей теории переселений проверить, могла ли в результате таких переселений из карты, которая есть в распоряжении «Разузнай» получиться карта, которую нашли археологи. Помогите им — напишите программу, которая будет это делать.
Выходные данные
Если гипотеза историков подтверждается, то в выходной файл выведите количество этапов переселения народов и дальше сами эти этапы, в результате которых из карты историков получается карта археологов. Каждый этап должен быть описан четырьмя числами — x1, y1, x2, y2 (координатами углов квадрата, который переселяется). Обратите внимание, что добиваться минимального количества переселений всех народов, или же минимального количества этапов не требуется. Важно, чтобы общее число этапов не превышало 10000 (математики из общества «Докажи» доказали, что в указанных ограничениях это всегда возможно).
Если гипотеза историков неверна, т.е. из карты историков карта археологов с помощью только таких переселений получиться не могла, то выведите в выходной файл одно число –1 (минус один).