Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 405 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: << 29 30 31 32 33 34 35 >> Отображать по:
#1316
Школы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Во взвешенном графе необходимо найти два минимальных остовных дерева.

С целью подготовки к проведению олимпиады по информатике мэр решил обеспечить надежным электроснабжением все школы города. Для этого необходимо провести линию электропередач от альтернативного источника электроэнергии “Майбуття” к одной из школ города (к какой неважно), а также соединить линиямии электропередач некоторые школы между собой.

Считается, что школа имеет надежное электроснабжение, если она напрямую связана с источником “Майбуття”, либо с одной из тех школ, которые имеют надежное электроснабжение.

Известна стоимость соединения между некоторыми парами школ. Мэр города решил выбрать одну из двух наиболее экономичных схем электроснабжения (стоимость схемы равняется сумме стоимостей соединений пар школ).

Напишите программу, которая вычисляет стоимость двух наиболее экономных схем альтернативного электроснабжения школ.

Входные данные

В первой строке входного файла находятся два натуральных числа, разделенных пробелом:N (3 ≤ N ≤ 100), количество школ в городе, и M – количество возможных соединений между ними. В каждой из последующих M строк находятся по три числа: Ai, Bi, Ci, разделенных пробелами, где Ci – стоимость прокладки линии электроснабжения (1 ≤ Ci ≤ 300) от школы Ai до школы Bi (i=1,2,…,N).

Выходные данные

В единственной строке выходного файла должны содержаться два натуральных числа S1 и S2, разделенных пробелом – две наименьшие стоимости схем (S1 ≤ S2). S1=S2 тогда и только тогда, когда существует несколько схем надежного электроснабжения наименьшей стоимости.

Гарантируется, что для входных данных существует две различные схемы надёжного электроснабжения.

Примеры
Входные данные
5 8
1 3 75
3 4 51
2 4 19
3 2 95
2 5 42
5 4 31
1 2 9
3 5 66
Выходные данные
110 121
#1317
Квадрат
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
8 megabytes
X1,Y1), (X2,Y2), (X3,Y3). Найти длину L стороны квадрата минимальной площади, в который можно поместить этот треугольник так, чтобы все вершины треугольника находились внутри квадрата либо на его сторонах.

Составьте программу, которая по координатам вершин треугольника находит длину L стороны квадрата минимальной площади, в который можно поместить этот треугольник. L достаточно найти с точностью 10-4.

Входные данные

Файл содержит в одной строке действительные числа X1 Y1 X2 Y2 X3 Y3, разделенные пробелами, – координаты вершин треугольника (-10000 X1, Y1, X2, Y2, X3, Y3 10000).

Выходные данные

Файл должен содержать одно число - длину L стороны искомого квадрата.

Примеры
Входные данные
0.0 0.0 1.1 0.0 0.0 1.1
Выходные данные
1.100000000
#1337
Компьютерная сеть
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

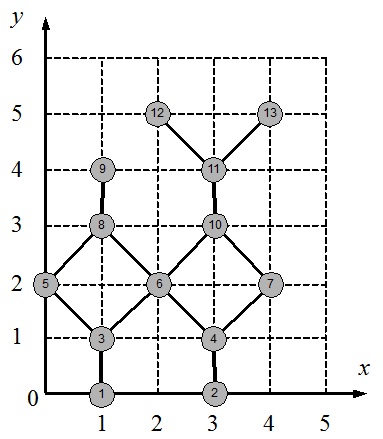
Для проведения олимпиады школьников по информатике требуется соединить компьютеры в сеть. Организаторы олимпиады разработали схему соединения компьютеров. В соответствии с этой схемой некоторые пары компьютеров должны быть соединены кабелем, и сигнал сможет дойти по кабелям от любого компьютера до любого другого, возможно, через другие компьютеры.

Некоторые компьютеры могут быть соединены циклически. Цикл называется простым, если каждый компьютер из этого цикла соединён ровно с двумя другими компьютерами этого цикла, и в этот цикл никакой кабель не входит более одного раза. Некоторые кабели могут не входить ни в какой цикл.

Известно, что в разработанной схеме никакой кабель не принадлежит двум простым циклам одновременно.

Организаторам олимпиады поручено разместить компьютеры в зале соревнований. При размещении должны выполняться следующие условия:

1.Компьютеры размещаются на плоскости в точках с целочисленными координатами.

2.Координаты компьютеров x и y лежат в диапазоне 0 ≤ x, y ≤ 106.

3.Никакие два компьютера не располагаются в одной точке.

4.Кабели являются отрезками прямых.

5.Кабели не пересекаются между собой и не проходят через точки размещения компьютеров, к которым они не подключены.

Требуется написать программу, выполняющую размещение компьютеров по заданному описанию схемы.

Входные данные

В первой строке входного файла содержатся числа N и M — количество компьютеров и количество кабелей в схеме (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 200 000). В последующих M строках содержатся пары чисел, разделенных пробелами. Каждая такая пара описывает один кабель, числа представляют собой номера соединенных компьютеров. Компьютеры пронумерованы от 1 до N. Никакая пара не встречается дважды, и никакой кабель не соединяет компьютер с самим собой.

Выходные данные

Выходной файл должен содержать N строк. Строка с номером i должна содержать координаты i-го компьютера, разделенные пробелом. Сначала выводится координата x, затем y. Разрешается вывести любой вариант размещения компьютеров, при котором выполняются условия 1–5.

Примечания

Решения, корректно работающие при отсутствии циклов, будут оцениваться из 40 баллов.

Решения, корректно работающие при наличии только одного цикла, будут оцениваться из 60 баллов.

Пример входных и выходных данных

Ввод

 Вывод

13 14

11 12

11 13

1 3

3 5

5 8

8 9

8 6

6 3

4 6

4 2

6 10

10 11

10 7

7 4

1 0

3 0

1 1

3 1

0 2

2 2

4 2

1 3

1 4

3 3

3 4

2 5

4 5


#1338
НГУ-стройка
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Заданы параллелепипеды с целочисленными координатами. Необходимо выбрать минимальный набор параллелепипедов, покрывающих горизонтальный слой.

Над ареной огромного спортивного комплекса Независимого Главного Университета (НГУ) решили построить перекрытие. Перекрытие будет построено по клеевой технологии и состоять из склеенных друг с другом блоков. Блок представляет собой легкий прямоугольный параллелепипед. Два блока можно склеить, если они соприкасаются перекрывающимися частями боковых граней ненулевой площади.

НГУ представил план комплекса, имеющий вид прямоугольника размером W на L. При этом один из углов прямоугольника находится в начале системы координат, а другой имеет координаты (W, L). Стены комплекса параллельны осям координат.

Подрядчики известили НГУ, что они готовы к определенному сроку изготовить блоки и установить их. Для каждого блока фиксировано место его возможного монтажа, совпадающее по размерам с этим блоком. Места выбраны так, что ребра блоков параллельны осям координат. Места монтажа блоков не пересекаются.


По техническим условиям перекрытие должно состоять из такого набора склеенных блоков, который содержит сплошной горизонтальный слой ненулевой толщины. Торопясь ввести комплекс в эксплуатацию, НГУ решил построить перекрытие из минимально возможного числа блоков.

Требуется написать программу, которая позволяет выбрать минимальное число блоков, которые, будучи установленными на указанных подрядчиками местах, образуют перекрытие, либо определить, что этого сделать невозможно. Высота, на которой образуется перекрытие, не имеет значения.

Входные данные

В первой строке входного файла указаны три целых числа: N — количество возможных блоков (1 ≤ N ≤ 105) и размеры комплекса W и L (1 ≤ W, L ≤ 104). Каждая из последующих N строк описывает место монтажа одного блока, определяемое координатами противоположных углов: (x1, y1, z1) и (x2, y2, z2), при этом 0 ≤ x1 < x2 ≤ W, 0 ≤ y1 < y2 ≤ L, 0 ≤ z1 < z2 ≤ 109. Все числа во входном файле целые и разделяются пробелами или переводами строк.

Гарантируется, что места установки блоков не пересекаются друг с другом.

Выходные данные

Первая строка выходного файла должна содержать либо слово «YES», если перекрытие возможно построить, иначе — слово «NO». В первом случае вторая строка выходного файла должна содержать минимальное число блоков, образующих перекрытие, а последующие строки — номера этих блоков, в соответствии с порядком, в котором они перечислены во входном файле.

Если возможно несколько минимальных наборов блоков, выведите любой из них.

Примечания

Решения, корректно работающие в случае, когда все числа во входном файле не превышают 100, будут оцениваться из 40 баллов.

Примеры
Входные данные
1 10 10
0 0 0 10 10 10
Выходные данные
YES
1
1
Входные данные
2 10 10
0 0 0 10 5 5
0 5 5 10 10 10
Выходные данные
NO
#1339
Цифры и числа
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Как много открытий можно сделать, исследуя числа и составляющие их цифры!

Петя очень любит арифметику, и кроме домашних заданий он постоянно придумывает дополнительные задачи. Однажды он стал прибавлять к натуральным числам сумму составляющих их цифр. Петя обнаружил, что некоторые числа, например 20, не могут быть получены из других чисел в результате такого действия. Эти числа ему не понравились, и он назвал их некрасивыми.

Позже, когда Петя начал изучать информатику, те же исследования он стал проводить с натуральными числами в двоичной системе счисления. Например, двоичное число 1110­2 (в десятичной системе — 14) можно получить из числа 11002 (в десятичной системе — 12), прибавив к последнему сумму его цифр:

11002 + 102 = 11102.

Петя решил исследовать множество двоичных некрасивых чисел. Первые пять некрасивых чисел он нашел без труда: 1 = 12, 4 = 1002, 6 = 1102, 13 = 11012, 15 = 11112. Продолжить работу он собирается с помощью компьютера.

Требуется написать программу, которая определяет количество двоичных некрасивых чисел, не превосходящих заданного числа n.

Входные данные

В первой строке входного файла содержится число n, записанное в десятичной системе счисления (1 ≤ n ≤ 1018).

Выходные данные

В единственной строке выходного файла должно содержаться единственное число — количество двоичных некрасивых чисел, не превосходящих n.

Примечание

Решения, корректно работающие при n ≤ 106, будут оцениваться из 40 баллов.

Примеры
Входные данные
17
Выходные данные
5
Входные данные
18
Выходные данные
6
Страница: << 29 30 31 32 33 34 35 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест