В традиционной музыке используются музыкальные звуки из некоторого набора, именуемого звукорядом. Звуки звукоряда принято группировать в октавы, в каждой из которых 12 звуков. Порядковый номер звука в пределах одной октавы назовем нотой. Таким образом, каждый звук можно задать парой чисел – номером октавы и номером ноты. Номер октавы \(К\) – произвольное целое число, номер ноты \(N\) принимает значение из интервала [01,12]. Звуки можно обозначать этими двумя числами, записанными рядом без пробелов (второе число всегда двузначное). Эту запись назовем кодом \(Q\). Например, \(Q\) = –108 для (–1)-й октавы, восьмой ноты. Значение \(Z\), определяемое по формуле \(Z = K\times 12 + N\) назовем абсолютным номером \(Z\) звука в звукоряде (для приведенного выше примера \(Z = –4\)).
Набор всех звуков, ноты которых принадлежат заданному подмножеству \(P\) номеров нот, назовем гармонией \(G\). Это означает, что любой звук с абсолютным номером \(Z = K\times 12 + n\), где \(n\) – номер ноты из \(P\), принадлежит этой гармонии при любом значении \(K\). Отсюда следует, что гармония однозначно определяется указанием \(P\). Две гармонии назовем эквивалентными, если при прибавлении некоторого одного и того же целого числа ко всем абсолютным номерам звуков первой гармонии получаются все элементы второй гармонии. Ограничимся рассмотрением только таких наборов гармоний, в которые наряду с каждой из гармоний входят и все эквивалентные ей. Для описания набора такого вида достаточно указать из каждой совокупности эквивалентных по одной гармонии \(G_i\) или соответствующему ей подмножеству \(P_i\). Базой \(B\) набора гармоний назовем совокупность всех таких \(P_i\).
Всякую совокупность одновременно звучащих звуков (не менее двух) будем называть аккордом \(A\). Для некоторого заданного набора гармоний назовем гармонией аккорда \(A\) такую гармонию \(G\) из него, что все звуки аккорда \(A\) принадлежат \(G\).
Будем говорить, что некоторый звук в тему для некоторого аккорда, если этот звук принадлежит хотя бы одной гармонии из множества всех гармоний этого аккорда.
Последовательное звучание произвольных звуков назовем мелодией. Каждому звуку мелодии может быть сопоставлен аккорд в порядке исполнения мелодии. Будем считать мелодию благозвучной для этой последовательности аккордов, если каждый ее звук оказывается в тему для соответствующего ему аккорда. Кучерявостью мелодии назовем сумму модулей разностей абсолютных номеров \(Z\) последовательно исполняемых звуков данной мелодии.
Пусть даны: база \(B\) набора гармоний, последовательность аккордов \(A\) и начальный звук \(Q\). Требуется написать программу, находящую наименее кучерявую из всех благозвучных мелодий, начинающихся с этого звука.
Выходные данные
В первую строку выходного файла следует вывести минимально возможную кучерявость среди всех мелодий, удовлетворяющих описанным выше требованиям. Оставшиеся строки должны содержать \(L\) целых чисел — коды \(Q\) звуков, составляющих соответствующую мелодию. Если вариантов мелодий несколько, нужно вывести любую из них. Для заданных во входном файле данных всегда будет существовать хотя бы одна благозвучная мелодия.
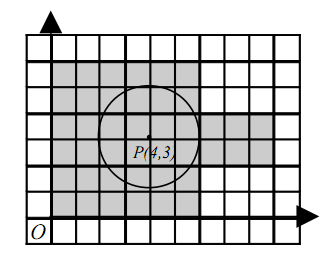 Требуется написать программу, перечисляющую прямоугольники, удаленные от \(P\) на расстояние, не превосходящее \(L\). Прямоугольники должны быть перечислены в порядке неубывания этого расстояния.
Требуется написать программу, перечисляющую прямоугольники, удаленные от \(P\) на расстояние, не превосходящее \(L\). Прямоугольники должны быть перечислены в порядке неубывания этого расстояния.